《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

11. 已知$F_1,F_2$分别是椭圆$E:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a ＞ b ＞ 0)$的左、右焦点，$M$是椭圆短轴的端点，点$N$在椭圆上，若$\overrightarrow{MF_1}=3\overrightarrow{NF_2}$，则椭圆$E$的离心率为（ ）
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{6}}{3}$

答案： C 由题设知，$F_{1}(-c,0)$，$F_{2}(c,0)$，
由对称性可设$M(0,b)$，$N(x,y)$，
$\therefore\overrightarrow{MF_{1}}=(-c,-b)$，$\overrightarrow{NF_{2}}=(c - x,-y)$，
又$\overrightarrow{MF_{1}}=3\overrightarrow{NF_{2}}$，$\therefore\begin{cases}-c = 3c - 3x\\-b=-3y\end{cases}$，即$\begin{cases}x=\frac{4c}{3}\\y=\frac{b}{3}\end{cases}$，
又$N$在椭圆上，
$\therefore\frac{16c^{2}}{9a^{2}}+\frac{b^{2}}{9b^{2}}=1$，可得$e=\frac{\sqrt{2}}{2}$。故选C。

12. (多选)(2024·江苏扬州大学附属中学月考)已知椭圆$\Omega:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a ＞ b ＞ 0)$，则下列结论正确的是（ ）
A. 若$a = 2b$，则$\Omega$的离心率为$\frac{\sqrt{2}}{2}$
B. 若$\Omega$的离心率为$\frac{1}{2}$，则$\frac{b}{a}=\frac{\sqrt{3}}{2}$
C. 若$F_1,F_2$为$\Omega$的两个焦点，直线$l$过点$F_1$且与$\Omega$交于点$A,B$，则$\triangle ABF_2$的周长为$4a$
D. 若$A_1,A_2$分别为$\Omega$的左、右顶点，$P$为$\Omega$上异于点$A_1,A_2$的任意一点，则$PA_1$，$PA_2$的斜率之积为$-\frac{b^{2}}{a^{2}}$

答案： BCD 选项A，离心率$e=\frac{c}{a}=\sqrt{\frac{c^{2}}{a^{2}}}=\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}=\sqrt{1-\frac{b^{2}}{a^{2}}}$，若$a = 2b$，则$e=\sqrt{1-\frac{b^{2}}{a^{2}}}=\sqrt{1-\frac{b^{2}}{(2b)^{2}}}=\frac{\sqrt{3}}{2}$，所以A不正确；选项B，若离心率$e=\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{1}{2}$，则$\frac{b}{a}=\frac{\sqrt{3}}{2}$，所以B正确；选项C，根据椭圆的定义可知C正确；选项D，设$P(x_{0},y_{0})$，则$\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}=1$，由椭圆方程可知$A_{1}(-a,0)$，$A_{2}(a,0)$，所以$k_{PA_{1}}\cdot k_{PA_{2}}=\frac{y_{0}}{x_{0}+a}\cdot\frac{y_{0}}{x_{0}-a}=\frac{y_{0}^{2}}{x_{0}^{2}-a^{2}}=\frac{b^{2}(1-\frac{x_{0}^{2}}{a^{2}})}{x_{0}^{2}-a^{2}}=-\frac{b^{2}}{a^{2}}$，所以D正确。故选BCD。

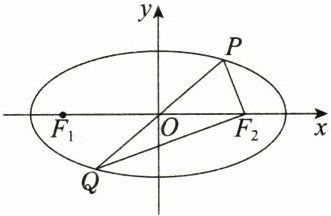
13. 如图，已知椭圆$E:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a ＞ b ＞ 0)$ 的左、右焦点分别为$F_1,F_2$，过坐标原点的直线交$E$于$P,Q$两点，且$PF_2\perp F_2Q$，且$S_{\triangle PF_2Q}=\frac{1}{2}a^{2}$，$|PF_2|+|F_2Q| = 4$，则$E$的标准方程为______________.

答案：
$\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$
解析 如图所示，连接$PF_{1}$，$QF_{1}$。
因为$\vert OP\vert=\vert OQ\vert$，$\vert OF_{1}\vert=\vert OF_{2}\vert$，所以四边形$PF_{1}QF_{2}$是平行四边形，所以$\vert PF_{1}\vert=\vert QF_{2}\vert$，$\vert PF_{2}\vert=\vert QF_{1}\vert$。
又因为$PF_{2}\perp F_{2}Q$，
所以平行四边形$PF_{1}QF_{2}$是矩形。
设$\vert PF_{1}\vert=m$，$\vert PF_{2}\vert=n$，
由题意得$\begin{cases}m + n = 2a = 4\\m^{2}+n^{2}=4c^{2}\\\frac{1}{2}mn=\frac{1}{2}a^{2}\end{cases}$，解得$\begin{cases}a = 2\\c=\sqrt{2}\end{cases}$，则$b^{2}=a^{2}-c^{2}=2$，所以$E$的标准方程为$\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$。

14. 若两个椭圆的离心率相等，则称它们为“相似椭圆”. 在直角坐标系$xOy$中，已知椭圆$C_1:\frac{x^{2}}{6}+\frac{y^{2}}{3}=1$，$A_1,A_2$分别为椭圆$C_1$的左、右顶点. 椭圆$C_2$以线段$A_1A_2$为短轴且与椭圆$C_1$为“相似椭圆”.
(1)求椭圆$C_2$的方程；
(2)设$P$为椭圆$C_2$上异于$A_1,A_2$的任意一点，过$P$作$PQ\perp x$轴，垂足为$Q$，线段$PQ$交椭圆$C_1$于点$H$. 求证：$H$为$\triangle PA_1A_2$的垂心.

答案： 解 （1）由题意可知$A_{1}(-\sqrt{6},0)$，$A_{2}(\sqrt{6},0)$，椭圆$C_{1}$的离心率$e=\frac{\sqrt{2}}{2}$。
设椭圆$C_{2}$的方程为$\frac{y^{2}}{a^{2}}+\frac{x^{2}}{b^{2}}=1(a\gt b\gt0)$，则$b=\sqrt{6}$，
$\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{\sqrt{2}}{2}$，解得$a^{2}=12$，$b^{2}=6$，
所以椭圆$C_{2}$的方程为$\frac{y^{2}}{12}+\frac{x^{2}}{6}=1$。
（2）证明：设$H(x,y)$，$P(x_{0},y_{0})(y_{0}\neq0)$，将$P(x_{0},y_{0})$代入$\frac{y^{2}}{12}+\frac{x^{2}}{6}=1$得$y_{0}^{2}=12 - 2x_{0}^{2}$，
将$x = x_{0}$代入椭圆$\frac{x^{2}}{6}+\frac{y^{2}}{3}=1$，得$y^{2}=3-\frac{x_{0}^{2}}{2}=\frac{y_{0}^{2}}{4}$，
因为$P$，$H$在$x$轴的同侧，所以$y=\frac{y_{0}}{2}$，
所以$H(x_{0},\frac{y_{0}}{2})$，
所以$k_{A_{2}P}\cdot k_{A_{1}H}=\frac{y_{0}}{x_{0}-\sqrt{6}}\cdot\frac{\frac{1}{2}y_{0}}{x_{0}+\sqrt{6}}=\frac{y_{0}^{2}}{2(x_{0}^{2}-6)}=\frac{12 - 2x_{0}^{2}}{2(x_{0}^{2}-6)}=-1$，所以$A_{2}P\perp A_{1}H$，
又$A_{2}A_{1}\perp PH$，所以$H$为$\triangle PA_{1}A_{2}$的垂心。

15. (文化情境命题)数学家蒙日发现：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，且圆半径的平方等于长半轴、短半轴的平方和，此圆被命名为该椭圆的蒙日圆. 若椭圆$\frac{x^{2}}{12}+\frac{y^{2}}{b^{2}}=1(b^{2}＜12)$的蒙日圆为$x^{2}+y^{2}=20$，则该椭圆的离心率为（ ）
A. $\frac{\sqrt{3}}{3}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{6}}{3}$

答案： A 由题意得$12 + b^{2}=20$，即$b^{2}=8$，所以$c=\sqrt{a^{2}-b^{2}}=\sqrt{12 - 8}=2$，则椭圆的离心率$e=\frac{c}{a}=\frac{2}{2\sqrt{3}}=\frac{\sqrt{3}}{3}$。故选A。