《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

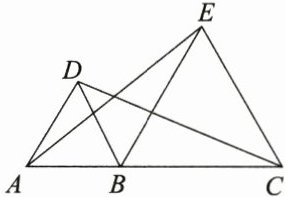
10. 如图，$\triangle ABD$和$\triangle BCE$是在直线$AC$同侧的两个等边三角形. 试用坐标法证明：$|AE| = |CD|$.

答案：
证明 如图所示，以$B$点为坐标原点，取$AC$所在直线为$x$轴，建立平面直角坐标系$xOy$. 设$\triangle ABD$和$\triangle BCE$的边长分别为$a$和$c$. 则$A(-a,0)$，$C(c,0)$，$E(\frac{c}{2},\frac{\sqrt{3}c}{2})$，$D(-\frac{a}{2},\frac{\sqrt{3}a}{2})$，由两点间的距离公式，得$|AE|=\sqrt{(\frac{c}{2}+a)^{2}+(\frac{\sqrt{3}c}{2}-0)^{2}}=\sqrt{a^{2}+ac + c^{2}}$，$|CD|=\sqrt{(c+\frac{a}{2})^{2}+(0-\frac{\sqrt{3}a}{2})^{2}}=\sqrt{a^{2}+ac + c^{2}}$，所以$|AE| = |CD|$.

11. 已知菱形$ABCD$的对角线$BD$与$x$轴平行，$D(-3,1),A(-1,0)$，则点$C$的坐标为（ ）
A. $(-1,2)$
B. $(-2,1)$
C. $(-1,1)$
D. $(2,2)$

答案： A $\because$四边形$ABCD$为菱形，$BD// x$轴，$\therefore AC\perp x$轴，$\therefore$可设$C(-1,t)(t\neq0)$，$\because|AD| = |CD|$，$\therefore\sqrt{(-3 + 1)^{2}+(1 - 0)^{2}}=\sqrt{(-3 + 1)^{2}+(1 - t)^{2}}$，解得$t = 0$（舍）或$t = 2$，$\therefore C(-1,2)$.

12.（多选）已知直线$l$经过点$P(3,1)$，且被两条平行直线$l_1:x + y + 1 = 0$和$l_2:x + y + 6 = 0$截得的线段长为 5，则直线$l$的方程可以为（ ）
A. $x = 2$
B. $x = 3$
C. $y = 1$
D. $y = 2$

答案： BC 若直线$l$的斜率不存在，则直线$l$的方程为$x = 3$，此时与$l_{1}$，$l_{2}$的交点分别为$A(3,-4)$，$B(3,-9)$，截得的线段$AB$的长$|AB|=|-4 + 9| = 5$，符合题意；若直线$l$的斜率存在，则设直线$l$的方程为$y = k(x - 3)+1$，由$\begin{cases}y = k(x - 3)+1\\x + y+1 = 0\end{cases}$，得交点$A(\frac{3k - 2}{k + 1},-\frac{4k - 1}{k + 1})$，由$\begin{cases}y = k(x - 3)+1\\x + y+6 = 0\end{cases}$，得交点$B(\frac{3k - 7}{k + 1},-\frac{9k - 1}{k + 1})$，由$|AB| = 5$，得$(\frac{3k - 2}{k + 1}-\frac{3k - 7}{k + 1})^{2}+(-\frac{4k - 1}{k + 1}+\frac{9k - 1}{k + 1})^{2}=5^{2}$，解得$k = 0$，即所求的直线方程为$y = 1$. 综上可知，所求直线$l$的方程为$x = 3$或$y = 1$，故选 BC.

13. 在平面直角坐标系内，到点$A(1,2),B(1,5),C(3,6),D(7,-1)$的距离之和最小的点的坐标是_______.

答案： $(2,4)$
解析 取平面上任一点$M$，因为$|MA|+|MC|\geqslant|AC|$，当且仅当点$M$在线段$AC$上时取等号；同理$|MB|+|MD|\geqslant|BD|$，当且仅当点$M$在线段$BD$上时取等号. 连接$AC$，$BD$交于一点$M$，则点$M$即为所求. 又$k_{AC}=\frac{6 - 2}{3 - 1}=2$，$\therefore$直线$AC$的方程为$y - 2 = 2(x - 1)$，即$2x - y = 0$①. 又$k_{BD}=\frac{5-(-1)}{1 - 7}=-1$，$\therefore$直线$BD$的方程为$y - 5=-(x - 1)$，即$x + y - 6 = 0$②. 联立①②得$\begin{cases}2x - y = 0\\x + y - 6 = 0\end{cases}$，解得$\begin{cases}x = 2\\y = 4\end{cases}$，$\therefore$点$M$的坐标为$(2,4)$.

14. 已知正三角形$ABC$的边长为$a$，在平面$ABC$上求一点$P$，使$|PA|^2 + |PB|^2 + |PC|^2$最小，并求此最小值.

答案：
解 以$BC$所在直线为$x$轴，以线段$BC$的中点为原点，建立直角坐标系，如图所示. $\because$正三角形$ABC$的边长为$a$，$\therefore B(-\frac{a}{2},0)$，$C(\frac{a}{2},0)$，$A(0,\frac{\sqrt{3}a}{2})$. 设$P(x,y)$，由两点间的距离公式，得$|PA|^{2}+|PB|^{2}+|PC|^{2}=x^{2}+(y-\frac{\sqrt{3}a}{2})^{2}+(x+\frac{a}{2})^{2}+y^{2}+(x-\frac{a}{2})^{2}+y^{2}=3x^{2}+3y^{2}-\sqrt{3}ay+\frac{5a^{2}}{4}=3x^{2}+3(y-\frac{\sqrt{3}a}{6})^{2}+a^{2}\geqslant a^{2}$，当且仅当$x = 0$，$y=\frac{\sqrt{3}a}{6}$时，等号成立. 故所求最小值为$a^{2}$，此时点$P$的坐标为$(0,\frac{\sqrt{3}a}{6})$.

15.（逻辑推理）（2023·河南平顶山联考）费马点是指三角形内到三角形三个顶点距离之和最小的点，当三角形三个内角均小于$120^{\circ}$时，费马点与三个顶点连线正好三等分费马点所在的周角，即该点所对三角形三边的张角相等，均为$120^{\circ}$. 根据以上性质，已知$A(-2,0),B(2,0),C(0,4)$，$P$为$\triangle ABC$内一点，记$f(P)=|PA| + |PB| + |PC|$，则$f(P)$的最小值为（ ）
A. $2\sqrt{3}$
B. $4 + 2\sqrt{3}$
C. $4 + \sqrt{3}$
D. $2 + \sqrt{3}$

答案：
B 设$O(0,0)$为坐标原点，由$A(-2,0)$，$B(2,0)$，$C(0,4)$，知$|AC| = |BC| = 2\sqrt{5}$，且$\triangle ABC$为锐角三角形，因此，费马点$M$在线段$OC$上，设$M(0,h)$，如图，则$\triangle MAB$为顶角是$120^{\circ}$的等腰三角形，故$h = |OB|\tan30^{\circ}=\frac{2\sqrt{3}}{3}$，所以$f(P)\geqslant f(M)=|MA|+|MB|+|MC|=2h + 2h+4 - h=4 + 2\sqrt{3}$，则$f(P)$的最小值为$4 + 2\sqrt{3}$. 故选 B.