2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 已知两直线的方向向量分别为$\boldsymbol{a},\boldsymbol{b}$,则下列选项中能使两直线垂直的为( )
A. $\boldsymbol{a}=(1,0,0),\boldsymbol{b}=(-3,0,0)$
B. $\boldsymbol{a}=(0,1,0),\boldsymbol{b}=(1,0,1)$
C. $\boldsymbol{a}=(0,1,-1),\boldsymbol{b}=(0,-1,1)$
D. $\boldsymbol{a}=(1,0,0),\boldsymbol{b}=(-1,0,0)$
A. $\boldsymbol{a}=(1,0,0),\boldsymbol{b}=(-3,0,0)$
B. $\boldsymbol{a}=(0,1,0),\boldsymbol{b}=(1,0,1)$
C. $\boldsymbol{a}=(0,1,-1),\boldsymbol{b}=(0,-1,1)$
D. $\boldsymbol{a}=(1,0,0),\boldsymbol{b}=(-1,0,0)$
答案:
1.B 因为B选项中a=(0,1,0),b=(1,0,1),a.b=0×1+1×0+0×1=0,所以a⊥b,
2. 如果直线$l$的方向向量是$\boldsymbol{a}=(-2,0,1)$,且直线$l$上有一点$P$不在平面$\alpha$内,平面$\alpha$的法向量是$\boldsymbol{b}=(2,0,4)$,那么( )
A. $l\perp\alpha$
B. $l//\alpha$
C. $l\subset\alpha$
D. $l$与$\alpha$斜交
A. $l\perp\alpha$
B. $l//\alpha$
C. $l\subset\alpha$
D. $l$与$\alpha$斜交
答案:
2.B 因为a.b=−2×2+0×0+1×4=0,所以a⊥b,又因为直线l上有一点P不在平面α内, 所以l∝α,所以l///α.故选B.
3. 如图,在四棱锥$P - ABCD$中,$PB\perp$平面$ABCD$,$PB = AB = 2BC = 4$,$AB\perp BC$,则点$C$到直线$PA$的距离为( )

A. $2\sqrt{3}$
B. $2\sqrt{5}$
C. $\sqrt{2}$
D. $4$

A. $2\sqrt{3}$
B. $2\sqrt{5}$
C. $\sqrt{2}$
D. $4$
答案:
3.A 如图,以B为坐标原点,射线BC,BA, BP分别为x轴、y轴、x轴的非负半轴,建 立空间直角坐标系, 则C(2,0,0),A(0,4,0),P(0,0,4), 故PC=(2,0,−4),PA=(0,4,−4), PA.$\frac{.0.}{PC}$ 所以 |PA|"$\frac{16}{4\sqrt{2}}$=2√2, 故点C到直线PA的距离为 $\sqrt{PC²−(2\sqrt{2}2}$= $\sqrt{20−8}$=2$\sqrt{3}$.故选A.
则C(2,0,0),A(0,4,0),P(0,0,4), 故PC=(2,0,−4),PA=(0,4,−4), PA.$\frac{.0.}{PC}$ 所以 |PA|"$\frac{16}{4\sqrt{2}}$=2√2, 故点C到直线PA的距离为 $\sqrt{PC²−(2\sqrt{2}2}$= $\sqrt{20−8}$=2$\sqrt{3}$.故选A.
3.A 如图,以B为坐标原点,射线BC,BA, BP分别为x轴、y轴、x轴的非负半轴,建 立空间直角坐标系,
 则C(2,0,0),A(0,4,0),P(0,0,4), 故PC=(2,0,−4),PA=(0,4,−4), PA.$\frac{.0.}{PC}$ 所以 |PA|"$\frac{16}{4\sqrt{2}}$=2√2, 故点C到直线PA的距离为 $\sqrt{PC²−(2\sqrt{2}2}$= $\sqrt{20−8}$=2$\sqrt{3}$.故选A.
则C(2,0,0),A(0,4,0),P(0,0,4), 故PC=(2,0,−4),PA=(0,4,−4), PA.$\frac{.0.}{PC}$ 所以 |PA|"$\frac{16}{4\sqrt{2}}$=2√2, 故点C到直线PA的距离为 $\sqrt{PC²−(2\sqrt{2}2}$= $\sqrt{20−8}$=2$\sqrt{3}$.故选A. 4.(2024·安徽淮北期末)在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,若$E$为$A_{1}C_{1}$的中点,则直线$CE$垂直于( )
A. $BD$
B. $AC$
C. $A_{1}D$
D. $A_{1}A$
A. $BD$
B. $AC$
C. $A_{1}D$
D. $A_{1}A$
答案:
4.A 如图,以D为坐标原点,DA,DC, DD所在的直线分别为x,y,N轴,建立 空间直角坐标系Dxyz,设正方体的棱长 为1,则C(0,1,0),B(1,1,0),A(1,0,0), D(0,0,0),A,(1,0,1),E($\frac{1}{2}$,$\frac{1}{2}$,1),所 以CE=($\frac{1}{2}$,−$\frac{1}{2}$,1),AC=(−1,1,0),BD=(−1,−1,0),AD=(−1,0,−1),AA=(0,0,−1).因为CE.BD=0,CE.AC=−1≠0,CE.AD=−$\frac{3}{2}$≠0,CE.AA=−1≠0,所以CE⊥BD.故选A.
为1,则C(0,1,0),B(1,1,0),A(1,0,0), D(0,0,0),A,(1,0,1),E($\frac{1}{2}$,$\frac{1}{2}$,1),所 以CE=($\frac{1}{2}$,−$\frac{1}{2}$,1),AC=(−1,1,0),BD=(−1,−1,0),AD=(−1,0,−1),AA=(0,0,−1).因为CE.BD=0,CE.AC=−1≠0,CE.AD=−$\frac{3}{2}$≠0,CE.AA=−1≠0,所以CE⊥BD.故选A.
4.A 如图,以D为坐标原点,DA,DC, DD所在的直线分别为x,y,N轴,建立 空间直角坐标系Dxyz,设正方体的棱长
 为1,则C(0,1,0),B(1,1,0),A(1,0,0), D(0,0,0),A,(1,0,1),E($\frac{1}{2}$,$\frac{1}{2}$,1),所 以CE=($\frac{1}{2}$,−$\frac{1}{2}$,1),AC=(−1,1,0),BD=(−1,−1,0),AD=(−1,0,−1),AA=(0,0,−1).因为CE.BD=0,CE.AC=−1≠0,CE.AD=−$\frac{3}{2}$≠0,CE.AA=−1≠0,所以CE⊥BD.故选A.
为1,则C(0,1,0),B(1,1,0),A(1,0,0), D(0,0,0),A,(1,0,1),E($\frac{1}{2}$,$\frac{1}{2}$,1),所 以CE=($\frac{1}{2}$,−$\frac{1}{2}$,1),AC=(−1,1,0),BD=(−1,−1,0),AD=(−1,0,−1),AA=(0,0,−1).因为CE.BD=0,CE.AC=−1≠0,CE.AD=−$\frac{3}{2}$≠0,CE.AA=−1≠0,所以CE⊥BD.故选A. 5. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑$ABCD$中,$AB\perp$平面$BCD$,$BC\perp CD$,且$AB = BC = CD$,$M$为$AD$的中点,则异面直线$BM$与$CD$夹角的余弦值为( )
A. $\frac{\sqrt{2}}{3}$
B. $\frac{\sqrt{3}}{4}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{\sqrt{2}}{4}$
A. $\frac{\sqrt{2}}{3}$
B. $\frac{\sqrt{3}}{4}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{\sqrt{2}}{4}$
答案:
5.C 如图,将鳖臑ABCD放在正方体中, 可知其是由正方体的四个顶点构成的, 建立空间直角坐标系Bxy,设正方体的 棱长为2,则B(0,0,0),C(2,0,0),D(2, 2,0),M(1,1,1),所以BM=(1,1,1), CD=(0,2,0),所以cos<BM,CD>=|BBMM|.|CCDD|=$\frac{2}{3×2}$=$\frac{\sqrt{3}}{3}$. 因为异面直线夹角的范围为(0,$\frac{π}{2}$1, 所以异面直线BM与CD夹角的余弦值为$\frac{\sqrt{3}}{3}$.
棱长为2,则B(0,0,0),C(2,0,0),D(2, 2,0),M(1,1,1),所以BM=(1,1,1), CD=(0,2,0),所以cos<BM,CD>=|BBMM|.|CCDD|=$\frac{2}{3×2}$=$\frac{\sqrt{3}}{3}$. 因为异面直线夹角的范围为(0,$\frac{π}{2}$1, 所以异面直线BM与CD夹角的余弦值为$\frac{\sqrt{3}}{3}$.
5.C 如图,将鳖臑ABCD放在正方体中, 可知其是由正方体的四个顶点构成的, 建立空间直角坐标系Bxy,设正方体的
 棱长为2,则B(0,0,0),C(2,0,0),D(2, 2,0),M(1,1,1),所以BM=(1,1,1), CD=(0,2,0),所以cos<BM,CD>=|BBMM|.|CCDD|=$\frac{2}{3×2}$=$\frac{\sqrt{3}}{3}$. 因为异面直线夹角的范围为(0,$\frac{π}{2}$1, 所以异面直线BM与CD夹角的余弦值为$\frac{\sqrt{3}}{3}$.
棱长为2,则B(0,0,0),C(2,0,0),D(2, 2,0),M(1,1,1),所以BM=(1,1,1), CD=(0,2,0),所以cos<BM,CD>=|BBMM|.|CCDD|=$\frac{2}{3×2}$=$\frac{\sqrt{3}}{3}$. 因为异面直线夹角的范围为(0,$\frac{π}{2}$1, 所以异面直线BM与CD夹角的余弦值为$\frac{\sqrt{3}}{3}$. 6. 如图,已知动点$P$在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的体对角线$BD_{1}$(不含端点)上.设$\frac{D_{1}P}{D_{1}B}=\lambda$,若$\angle APC$为钝角,则实数$\lambda$的取值范围为( )

A. $(0,\frac{1}{3})$
B. $(0,\frac{1}{2})$
C. $(\frac{1}{3},1)$
D. $(\frac{1}{2},1)$

A. $(0,\frac{1}{3})$
B. $(0,\frac{1}{2})$
C. $(\frac{1}{3},1)$
D. $(\frac{1}{2},1)$
答案:
6.C 由题设,建立如图所示的空间直角坐 标系Dxyz, 设正方体ABCD−ABC:D的棱长为1, 则有A(1,0,0),B(1,1,0),C(0,1,0), D(0,0,1),DA=(1,0,−1 DC 1,−1),DB=(1,1,−1),则$\frac{),D}{DP}$=$\frac{(0,}{B}$=(λ,λ,一λ),
则有A(1,0,0),B(1,1,0),C(0,1,0), D(0,0,1),DA=(1,0,−1 DC 1,−1),DB=(1,1,−1),则$\frac{),D}{DP}$=$\frac{(0,}{B}$=(λ,λ,一λ),
∴PA=PD+DA=(−λ,−λ,λ)+(1,0,−1)=(1−λ,一λ,λ−1) PC=PD+$\frac{.}{D,C}$=(−λ,−λ,λ)+(0,1,−1)=(−λ,1−λ,λ−1).
∵∠APC为钝角,则cos∠APC<0,
∴PA.PC<O,
∴(1−λ)(−λ)+(−λ)(1−λ)+(λ−1)²=(λ−1)(3λ−1)<0,解得$\frac{1}{3}$∽<1,
∴λ的取值范围是($\frac{1}{3}$,1).故选C
6.C 由题设,建立如图所示的空间直角坐 标系Dxyz, 设正方体ABCD−ABC:D的棱长为1,
 则有A(1,0,0),B(1,1,0),C(0,1,0), D(0,0,1),DA=(1,0,−1 DC 1,−1),DB=(1,1,−1),则$\frac{),D}{DP}$=$\frac{(0,}{B}$=(λ,λ,一λ),
则有A(1,0,0),B(1,1,0),C(0,1,0), D(0,0,1),DA=(1,0,−1 DC 1,−1),DB=(1,1,−1),则$\frac{),D}{DP}$=$\frac{(0,}{B}$=(λ,λ,一λ),∴PA=PD+DA=(−λ,−λ,λ)+(1,0,−1)=(1−λ,一λ,λ−1) PC=PD+$\frac{.}{D,C}$=(−λ,−λ,λ)+(0,1,−1)=(−λ,1−λ,λ−1).
∵∠APC为钝角,则cos∠APC<0,
∴PA.PC<O,
∴(1−λ)(−λ)+(−λ)(1−λ)+(λ−1)²=(λ−1)(3λ−1)<0,解得$\frac{1}{3}$∽<1,
∴λ的取值范围是($\frac{1}{3}$,1).故选C
7. 如图所示,在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$AC\perp BC$,且$BC = 3$,$AC = 4$,$CC_{1}=3$,点$P$在棱$AA_{1}$上,且三棱锥$A - PBC$的体积为$4$,则直线$BC_{1}$与平面$PBC$所成角的正弦值等于( )

A. $\frac{\sqrt{10}}{4}$
B. $\frac{\sqrt{6}}{4}$
C. $\frac{\sqrt{10}}{5}$
D. $\frac{\sqrt{15}}{5}$

A. $\frac{\sqrt{10}}{4}$
B. $\frac{\sqrt{6}}{4}$
C. $\frac{\sqrt{10}}{5}$
D. $\frac{\sqrt{15}}{5}$
答案:
7.C 由已知得AA1⊥底面ABC,且 AC⊥BC,所以VA−PBC=VP−AβC=$\frac{1}{3}$× SABC×PA=$\frac{1}{3}$×$\frac{1}{2}$×3×4×PA=4, 解得PA=2.如图所示,以点C为坐标 原点,CB,CA,CC所在直线分别为x,y,N轴建立空间直角坐标系,则C(0,0,0),P(0,4,2),B(3,0,0),C(0,0,3),则CB=(3,0,0),,CP=(0,4,2),BC=(−3,0,3)),设平面PBC的法向量为n=(x,y,),则由{nn..CcBP==00,,可得{34xy+=20x,=0,得x=0,令y=1,得x= −2,所以n=(0,1,−2)为平面PBC的一个法向量,设直线BC,与平面PBC所成的角为0,则sinθ=|cos(n,BC>|=|n.BC|= |n||BC1| $\frac{1−61}{\sqrt{1²+(−2)²}x\sqrt{(−3)²+3²}}$ $\frac{\sqrt{10}}{5}$.故选C.
SABC×PA=$\frac{1}{3}$×$\frac{1}{2}$×3×4×PA=4, 解得PA=2.如图所示,以点C为坐标 原点,CB,CA,CC所在直线分别为x,y,N轴建立空间直角坐标系,则C(0,0,0),P(0,4,2),B(3,0,0),C(0,0,3),则CB=(3,0,0),,CP=(0,4,2),BC=(−3,0,3)),设平面PBC的法向量为n=(x,y,),则由{nn..CcBP==00,,可得{34xy+=20x,=0,得x=0,令y=1,得x= −2,所以n=(0,1,−2)为平面PBC的一个法向量,设直线BC,与平面PBC所成的角为0,则sinθ=|cos(n,BC>|=|n.BC|= |n||BC1| $\frac{1−61}{\sqrt{1²+(−2)²}x\sqrt{(−3)²+3²}}$ $\frac{\sqrt{10}}{5}$.故选C.
7.C 由已知得AA1⊥底面ABC,且 AC⊥BC,所以VA−PBC=VP−AβC=$\frac{1}{3}$×
 SABC×PA=$\frac{1}{3}$×$\frac{1}{2}$×3×4×PA=4, 解得PA=2.如图所示,以点C为坐标 原点,CB,CA,CC所在直线分别为x,y,N轴建立空间直角坐标系,则C(0,0,0),P(0,4,2),B(3,0,0),C(0,0,3),则CB=(3,0,0),,CP=(0,4,2),BC=(−3,0,3)),设平面PBC的法向量为n=(x,y,),则由{nn..CcBP==00,,可得{34xy+=20x,=0,得x=0,令y=1,得x= −2,所以n=(0,1,−2)为平面PBC的一个法向量,设直线BC,与平面PBC所成的角为0,则sinθ=|cos(n,BC>|=|n.BC|= |n||BC1| $\frac{1−61}{\sqrt{1²+(−2)²}x\sqrt{(−3)²+3²}}$ $\frac{\sqrt{10}}{5}$.故选C.
SABC×PA=$\frac{1}{3}$×$\frac{1}{2}$×3×4×PA=4, 解得PA=2.如图所示,以点C为坐标 原点,CB,CA,CC所在直线分别为x,y,N轴建立空间直角坐标系,则C(0,0,0),P(0,4,2),B(3,0,0),C(0,0,3),则CB=(3,0,0),,CP=(0,4,2),BC=(−3,0,3)),设平面PBC的法向量为n=(x,y,),则由{nn..CcBP==00,,可得{34xy+=20x,=0,得x=0,令y=1,得x= −2,所以n=(0,1,−2)为平面PBC的一个法向量,设直线BC,与平面PBC所成的角为0,则sinθ=|cos(n,BC>|=|n.BC|= |n||BC1| $\frac{1−61}{\sqrt{1²+(−2)²}x\sqrt{(−3)²+3²}}$ $\frac{\sqrt{10}}{5}$.故选C. 8. 已知点$E$在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的侧面$AA_{1}B_{1}B$内(含边界),$F$是$AA_{1}$的中点,若$D_{1}E\perp CF$,则$\tan\angle BCE$的最小值为( )
A. $\frac{\sqrt{5}}{5}$
B. $\sqrt{2}-1$
C. $\sqrt{3}-1$
D. $\frac{\sqrt{3}}{5}$
A. $\frac{\sqrt{5}}{5}$
B. $\sqrt{2}-1$
C. $\sqrt{3}-1$
D. $\frac{\sqrt{3}}{5}$
答案:
8.A 连接BE,由题得△BEC是直角三 角形,在Rt△BEC中,tan∠BCE= $\frac{EB}{BC}$,所以当EB取最小值时,tan∠BCE 最小. 设AA1=2,以A为原点,建立如图所示x 的空间直角坐标系, 则C(2,2,0),F(0,0,1),D(0,2,2).设E(x,0,x),所以CF=(−2,−2,1),DE=(x,−2,x−2), 因为DE⊥CF,所以CF.DE=−2x+x+2=0,即2x−x−2=0.取棱AB的中点M,则E点的轨迹为线段BM. 当BE⊥B1M时,BE最小,此时BE=$\frac{2\sqrt{5}}{5}$, 所以tan∠BCE=$\frac{EB}{BC}$=$\frac{\sqrt{5}}{5}$.故选A.
最小. 设AA1=2,以A为原点,建立如图所示x 的空间直角坐标系, 则C(2,2,0),F(0,0,1),D(0,2,2).设E(x,0,x),所以CF=(−2,−2,1),DE=(x,−2,x−2), 因为DE⊥CF,所以CF.DE=−2x+x+2=0,即2x−x−2=0.取棱AB的中点M,则E点的轨迹为线段BM. 当BE⊥B1M时,BE最小,此时BE=$\frac{2\sqrt{5}}{5}$, 所以tan∠BCE=$\frac{EB}{BC}$=$\frac{\sqrt{5}}{5}$.故选A.
8.A 连接BE,由题得△BEC是直角三 角形,在Rt△BEC中,tan∠BCE= $\frac{EB}{BC}$,所以当EB取最小值时,tan∠BCE
 最小. 设AA1=2,以A为原点,建立如图所示x 的空间直角坐标系, 则C(2,2,0),F(0,0,1),D(0,2,2).设E(x,0,x),所以CF=(−2,−2,1),DE=(x,−2,x−2), 因为DE⊥CF,所以CF.DE=−2x+x+2=0,即2x−x−2=0.取棱AB的中点M,则E点的轨迹为线段BM. 当BE⊥B1M时,BE最小,此时BE=$\frac{2\sqrt{5}}{5}$, 所以tan∠BCE=$\frac{EB}{BC}$=$\frac{\sqrt{5}}{5}$.故选A.
最小. 设AA1=2,以A为原点,建立如图所示x 的空间直角坐标系, 则C(2,2,0),F(0,0,1),D(0,2,2).设E(x,0,x),所以CF=(−2,−2,1),DE=(x,−2,x−2), 因为DE⊥CF,所以CF.DE=−2x+x+2=0,即2x−x−2=0.取棱AB的中点M,则E点的轨迹为线段BM. 当BE⊥B1M时,BE最小,此时BE=$\frac{2\sqrt{5}}{5}$, 所以tan∠BCE=$\frac{EB}{BC}$=$\frac{\sqrt{5}}{5}$.故选A. 9. 已知边长为$4$的正方形$ABCD$所在平面外一点$P$与正方形的中心$O$的连线$PO$垂直于平面$ABCD$,且$PO = 6$,则$PO$的中点$M$到$\triangle PBC$的重心$N$的距离为________.
答案:
9.$\frac{5}{3}$ 解析 依题意建立如图所示的空间直角坐 标系.由题意得M(0,0,3),N(0,$\frac{4}{3}$,2), 则MN=(0,$\frac{4}{3}$,−1). 于是|MN|= $\sqrt{0²+(\frac{4}{3}+(−1)²}$= $\frac{5}{3}$.故PO的中点M到△PBC的重心N的距离为$\frac{5}{3}$.
则MN=(0,$\frac{4}{3}$,−1). 于是|MN|= $\sqrt{0²+(\frac{4}{3}+(−1)²}$= $\frac{5}{3}$.故PO的中点M到△PBC的重心N的距离为$\frac{5}{3}$.
9.$\frac{5}{3}$ 解析 依题意建立如图所示的空间直角坐 标系.由题意得M(0,0,3),N(0,$\frac{4}{3}$,2),
 则MN=(0,$\frac{4}{3}$,−1). 于是|MN|= $\sqrt{0²+(\frac{4}{3}+(−1)²}$= $\frac{5}{3}$.故PO的中点M到△PBC的重心N的距离为$\frac{5}{3}$.
则MN=(0,$\frac{4}{3}$,−1). 于是|MN|= $\sqrt{0²+(\frac{4}{3}+(−1)²}$= $\frac{5}{3}$.故PO的中点M到△PBC的重心N的距离为$\frac{5}{3}$. 10. 如图,直三棱柱$ABC - A_{1}B_{1}C_{1}$的侧棱$AA_{1}=\sqrt{3}$,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC = 1$,则点$B_{1}$到平面$A_{1}BC$的距离为________.


答案:
10.$\frac{\sqrt{3}}{2}$ 解析 如图所示,建立空间直角坐标系, 则B(0,1,0),C(0,0,0),A1(1,0,$\sqrt{3}$), B,(0,1,$\sqrt{3}$),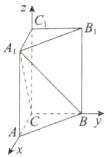
∴AB=(−1,1,−$\sqrt{3}$),AC=(−1,0, $\sqrt{3}$),AB=(−1,1,0). 设平面ABC的法向量为n=(x,y,), 则{nn.A=0'即−x+y−$\sqrt{3}$x=0, −x−$\sqrt{3}$x=0. 令x=1,得x=−$\sqrt{3}$,y=0,
∴n=(−$\sqrt{3}$,0,1). $\sqrt{3}$,0,1).
∴点B到平面ABC的距离d=$\frac{n.AB}{|n)}$=$\frac{\sqrt{3}}{2}$
10.$\frac{\sqrt{3}}{2}$ 解析 如图所示,建立空间直角坐标系, 则B(0,1,0),C(0,0,0),A1(1,0,$\sqrt{3}$), B,(0,1,$\sqrt{3}$),

∴AB=(−1,1,−$\sqrt{3}$),AC=(−1,0, $\sqrt{3}$),AB=(−1,1,0). 设平面ABC的法向量为n=(x,y,), 则{nn.A=0'即−x+y−$\sqrt{3}$x=0, −x−$\sqrt{3}$x=0. 令x=1,得x=−$\sqrt{3}$,y=0,
∴n=(−$\sqrt{3}$,0,1). $\sqrt{3}$,0,1).
∴点B到平面ABC的距离d=$\frac{n.AB}{|n)}$=$\frac{\sqrt{3}}{2}$
11.(2023·山西大同四校联考)如图,在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,底面是以$\angle ABC$为直角的等腰直角三角形,$AC = 2a$,$BB_{1}=3a$,$D$是$A_{1}C_{1}$的中点,点$E$在棱$AA_{1}$上,要使$CE\perp$平面$B_{1}DE$,则$AE =$________.


答案:
11.a或2a 解析 以B为坐标原点,BA,BC,BB1所 在的直线分别为x轴、y轴、N轴,建立如图 所示的空间直角坐标系,则B(0,0,3a), C(o'$\sqrt{2}$a,0).设E($\sqrt{2}$a,0,x)(0≤x≤3a), 则CE=($\sqrt{2}$a,−$\sqrt{2}$a,x),B.E.=($\sqrt{2}$a,0, x−3a).由题意得CE⊥$\frac{BE}{BE}$,则CE.BE=O,即2a²+N²−3az=0,解得x=a或2a,即AE=a或2a.
C(o'$\sqrt{2}$a,0).设E($\sqrt{2}$a,0,x)(0≤x≤3a), 则CE=($\sqrt{2}$a,−$\sqrt{2}$a,x),B.E.=($\sqrt{2}$a,0, x−3a).由题意得CE⊥$\frac{BE}{BE}$,则CE.BE=O,即2a²+N²−3az=0,解得x=a或2a,即AE=a或2a.
11.a或2a 解析 以B为坐标原点,BA,BC,BB1所 在的直线分别为x轴、y轴、N轴,建立如图 所示的空间直角坐标系,则B(0,0,3a),
 C(o'$\sqrt{2}$a,0).设E($\sqrt{2}$a,0,x)(0≤x≤3a), 则CE=($\sqrt{2}$a,−$\sqrt{2}$a,x),B.E.=($\sqrt{2}$a,0, x−3a).由题意得CE⊥$\frac{BE}{BE}$,则CE.BE=O,即2a²+N²−3az=0,解得x=a或2a,即AE=a或2a.
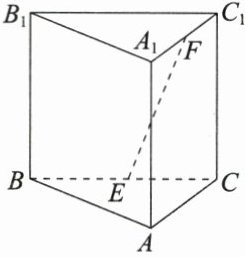
C(o'$\sqrt{2}$a,0).设E($\sqrt{2}$a,0,x)(0≤x≤3a), 则CE=($\sqrt{2}$a,−$\sqrt{2}$a,x),B.E.=($\sqrt{2}$a,0, x−3a).由题意得CE⊥$\frac{BE}{BE}$,则CE.BE=O,即2a²+N²−3az=0,解得x=a或2a,即AE=a或2a. 12. 如图,在正三棱柱$ABC - A_{1}B_{1}C_{1}$中,$AB = AA_{1}=2$,$E,F$分别是$BC,A_{1}C_{1}$的中点.设$D$是线段$B_{1}C_{1}$上的动点(包括两个端点),若直线$BD$与$EF$所成角的余弦值为$\frac{\sqrt{10}}{4}$,则线段$BD$的长为________.

答案:
12.2√2 解析 如图,以E为原点建立空间直角 坐标系, 则E(0,0,0),F($\frac{3}{2}$,$\frac{1}{2}$,2),B(0,−1, 一 0),设D(0,t,2)(−1≤t≤1),则EF= ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,2),BD=(0,t+1,2),设直线 BD与EF所成的角为θ,则cos0=||EEFF|.|BBDD|= |$\frac{t+1}{2}$+4| =$\frac{\sqrt{10}}{4}$,即23t²+14t−37=0,解得$\sqrt{5}$. $\sqrt{(t+1)²+4}$t=1或t=−$\frac{37}{23}$(舍去),所以BD=|BD|= $\sqrt{0²+2+2²}$=2√2.
一 0),设D(0,t,2)(−1≤t≤1),则EF= ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,2),BD=(0,t+1,2),设直线 BD与EF所成的角为θ,则cos0=||EEFF|.|BBDD|= |$\frac{t+1}{2}$+4| =$\frac{\sqrt{10}}{4}$,即23t²+14t−37=0,解得$\sqrt{5}$. $\sqrt{(t+1)²+4}$t=1或t=−$\frac{37}{23}$(舍去),所以BD=|BD|= $\sqrt{0²+2+2²}$=2√2.
12.2√2 解析 如图,以E为原点建立空间直角 坐标系, 则E(0,0,0),F($\frac{3}{2}$,$\frac{1}{2}$,2),B(0,−1,
 一 0),设D(0,t,2)(−1≤t≤1),则EF= ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,2),BD=(0,t+1,2),设直线 BD与EF所成的角为θ,则cos0=||EEFF|.|BBDD|= |$\frac{t+1}{2}$+4| =$\frac{\sqrt{10}}{4}$,即23t²+14t−37=0,解得$\sqrt{5}$. $\sqrt{(t+1)²+4}$t=1或t=−$\frac{37}{23}$(舍去),所以BD=|BD|= $\sqrt{0²+2+2²}$=2√2.
一 0),设D(0,t,2)(−1≤t≤1),则EF= ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,2),BD=(0,t+1,2),设直线 BD与EF所成的角为θ,则cos0=||EEFF|.|BBDD|= |$\frac{t+1}{2}$+4| =$\frac{\sqrt{10}}{4}$,即23t²+14t−37=0,解得$\sqrt{5}$. $\sqrt{(t+1)²+4}$t=1或t=−$\frac{37}{23}$(舍去),所以BD=|BD|= $\sqrt{0²+2+2²}$=2√2. 13. 如图,在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$\angle ABC=\frac{\pi}{2}$,$D$是棱$AC$的中点,且$AB = BC = BB_{1}=2$.
(1)求证:$AB_{1}//$平面$BC_{1}D$;
(2)求异面直线$AB_{1}$与$BC_{1}$所成角的大小.

(1)求证:$AB_{1}//$平面$BC_{1}D$;
(2)求异面直线$AB_{1}$与$BC_{1}$所成角的大小.

答案:
13.解
(1)证明:建立如图所示的空间 直角坐标系Bxy,则B(0,0,0), A(0,2,0),C(2,0,2),B(0,0,2), D(1,1,0), 因此AB=(0,−2,2),BC=(2, 0,2),BD=(1,1,0), 设平面BCD的一个法向量为n=(x,y,z),则 {BBCD..nn==00,,即{x2.x++y2=x=0,0,令x=1,则y=−1,x=−1, 故平面BCD的一个法向量为n=(1,−1,−1), 因为AB.n=0,所以AB⊥n,又因为AB1C平面BC1D,所以AB1//平面BC1D.
D(1,1,0), 因此AB=(0,−2,2),BC=(2, 0,2),BD=(1,1,0), 设平面BCD的一个法向量为n=(x,y,z),则 {BBCD..nn==00,,即{x2.x++y2=x=0,0,令x=1,则y=−1,x=−1, 故平面BCD的一个法向量为n=(1,−1,−1), 因为AB.n=0,所以AB⊥n,又因为AB1C平面BC1D,所以AB1//平面BC1D.
(2)由
(1)得AB=(0,−2,2),一C.=(2',0,2), AB.$\frac{BC,}{BC}$ 所以cos<AB,BC>=|AB||BC|=$\frac{0+0+4}{2\sqrt{2}×2\sqrt{2}}$=$\frac{1}{2}$,设异面直线AB与BC,所成的角为0,则cos0=$\frac{1}{2}$,由于0∈(0.'$\frac{π}{2}$],故θ=$\frac{π}{3}$, 即异面直线AB,与BC,所成角的大小为$\frac{π}{3}$.
13.解
(1)证明:建立如图所示的空间 直角坐标系Bxy,则B(0,0,0), A(0,2,0),C(2,0,2),B(0,0,2),
 D(1,1,0), 因此AB=(0,−2,2),BC=(2, 0,2),BD=(1,1,0), 设平面BCD的一个法向量为n=(x,y,z),则 {BBCD..nn==00,,即{x2.x++y2=x=0,0,令x=1,则y=−1,x=−1, 故平面BCD的一个法向量为n=(1,−1,−1), 因为AB.n=0,所以AB⊥n,又因为AB1C平面BC1D,所以AB1//平面BC1D.
D(1,1,0), 因此AB=(0,−2,2),BC=(2, 0,2),BD=(1,1,0), 设平面BCD的一个法向量为n=(x,y,z),则 {BBCD..nn==00,,即{x2.x++y2=x=0,0,令x=1,则y=−1,x=−1, 故平面BCD的一个法向量为n=(1,−1,−1), 因为AB.n=0,所以AB⊥n,又因为AB1C平面BC1D,所以AB1//平面BC1D. (2)由
(1)得AB=(0,−2,2),一C.=(2',0,2), AB.$\frac{BC,}{BC}$ 所以cos<AB,BC>=|AB||BC|=$\frac{0+0+4}{2\sqrt{2}×2\sqrt{2}}$=$\frac{1}{2}$,设异面直线AB与BC,所成的角为0,则cos0=$\frac{1}{2}$,由于0∈(0.'$\frac{π}{2}$],故θ=$\frac{π}{3}$, 即异面直线AB,与BC,所成角的大小为$\frac{π}{3}$.
查看更多完整答案,请扫码查看


