《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

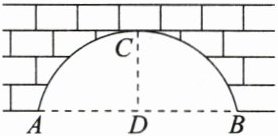
1. 如图，圆弧形拱桥的跨度$|AB| = 12$米，拱高$|CD| = 4$米，则拱桥所在圆的直径为（ ）

A. 15米
B. 13米
C. 9米
D. 6.5米

答案：
B 如图，设此圆弧形拱桥所在圆的圆心为O，半径为r，则由勾股定理得|OB|² = |OD|² + |BD|²，即r² = (r - 4)² + 6²，解得r = $\frac{13}{2}$，所以拱桥所在圆的直径为13米。

2. 设某公园外围成圆形，其所在曲线的方程可用$x^{2}+y^{2}-2x = 0$表示，在公园外两点$A(-2,0)$，$B(0,2)$与公园外围任意一点修建一处三角形舞台，则舞台面积的最小值为（ ）
A. $3-\sqrt{2}$
B. $3+\sqrt{2}$
C. $3-\frac{\sqrt{2}}{2}$
D. $\frac{3 - \sqrt{2}}{2}$

答案： A 因为直线$l_{AB}:x - y + 2 = 0$，公园外围圆的圆心为(1,0)，半径为1，则圆心到直线$l_{AB}$的距离为$d = \frac{|3|}{\sqrt{2}} = \frac{3\sqrt{2}}{2}$，所以AB边上的高的最小值为$\frac{3\sqrt{2}}{2} - 1$，所以三角形舞台面积$S_{min} = \frac{1}{2}×2\sqrt{2}×(\frac{3\sqrt{2}}{2} - 1) = 3 - \sqrt{2}$。

3. 小明家附近的一座桥是仿赵州桥建造的一座圆拱桥，已知在某个时间段，这座桥的水面跨度是20米，拱顶离水面4米，当水面上涨2米后，桥在水面的跨度为（ ）
A. 10米
B. $10\sqrt{2}$米
C. $6\sqrt{6}$米
D. $6\sqrt{5}$米

答案：
C 根据题意，建立如图所示的圆拱桥模型。设圆O的半径为R，当水面跨度是20米，拱顶离水面4米时，水面为AB，M为AB的中点，即|AB| = 20，|OM| = R - 4，由勾股定理，得|AM|² = ($\frac{|AB|}{2}$)² = |OA|² - |OM|²，即100 = R² - (R - 4)²，解得R = $\frac{29}{2}$。当水面上涨2米后水面为CD，N为CD的中点，此时|ON| = R - 2，由勾股定理，得|CD| = 2|CN| = 2$\sqrt{R^{2}-(R - 2)^{2}}$ = 6$\sqrt{6}$（米）。

4. 过点$M(1,2)$的直线$l$将圆$(x - 2)^{2}+y^{2}=9$分成两段弧，当其中的劣弧最短时，直线$l$的方程是（ ）
A. $x = 1$
B. $y = 1$
C. $x - 2y + 3 = 0$
D. $x - y + 1 = 0$

答案： C 由条件知点M在圆内，故当劣弧最短时，l应与过圆心与点M的直线垂直。设圆心为E，则E(2,0)，
∴$k_{EM} = \frac{2 - 0}{1 - 2} = - 2$，故直线l的斜率$k = \frac{1}{2}$，
∴直线l的方程为$y - 2 = \frac{1}{2}(x - 1)$，即$x - 2y + 3 = 0$。

5.（2023·沈阳期末）圆$x^{2}+y^{2}+2x - 4y + 1 = 0$关于直线$2ax - by + 2 = 0(a,b\in\mathbf{R})$对称，则$ab$的取值范围是（ ）
A. $(-\infty,\frac{1}{4}]$
B. $(0,\frac{1}{4}]$
C. $(-\frac{1}{4},0]$
D. $(-\infty,\frac{1}{4})$

答案： A 把圆的方程化为标准方程得$(x + 1)^{2}+(y - 2)^{2}=4$，
∴圆心坐标为(-1,2)，半径r = 2。根据题意可知，圆心在直线2ax - by + 2 = 0上，把圆心坐标代入直线方程得 - 2a - 2b + 2 = 0，即b = 1 - a。设$m = ab = a(1 - a)= - a^{2}+a = - (a - \frac{1}{2})^{2}+\frac{1}{4}$，
∴当$a = \frac{1}{2}$时，m有最大值，最大值为$\frac{1}{4}$，即ab的最大值为$\frac{1}{4}$，则ab的取值范围是$(-∞,\frac{1}{4}]$。故选A。

6. 台风中心从$A$地以每小时20 km的速度向东北方向移动，离台风中心30 km内的地区为危险地区，若城市$B$在$A$地正东40 km处，则城市$B$处于危险地区内的时间为（ ）
A. 0.5 h
B. 1 h
C. 1.5 h
D. 2 h

答案： B 以A为坐标原点，正东方向为x轴，正北方向为y轴建立平面直角坐标系，则B(40,0)，台风中心移动轨迹为$y = x(x≥0)$，而B点到射线$y = x(x≥0)$的距离$d = \frac{|40|}{\sqrt{2}} = 20\sqrt{2}＜30$，则直线$y = x$被圆$(x - 40)^{2}+y^{2}=30^{2}$截得的弦长为$2\sqrt{30^{2}-(20\sqrt{2})^{2}} = 20$，
∴城市B处于危险地区内的时间为$\frac{20}{20}=1h$，故选B。

7. 实数$x$，$y$满足方程$x + y - 4 = 0$，则$x^{2}+y^{2}$的最小值为_______.

答案： 8
解析 令$x^{2}+y^{2}=r^{2}(r＞0)$，则$x^{2}+y^{2}$的最小值为圆$x^{2}+y^{2}=r^{2}$与直线相切时的圆的半径的平方，所以$r_{min}=\frac{|0 + 0 - 4|}{\sqrt{1^{2}+1^{2}}}=2\sqrt{2}$，即$x^{2}+y^{2}$的最小值为8。

8. 已知隧道的截面是半径为4.0 m的半圆，车辆只能在道路中心线一侧行驶，一辆宽为2.7 m、高为2.5 m的货车_______驶入这个隧道.（填“能”或“不能”）

答案：
能
解析 以隧道截面半圆的圆心为坐标原点，半圆直径所在直线为x轴，建立如图所示的平面直角坐标系，则半圆方程为$x^{2}+y^{2}=16(y≥0)$。将$x = 2.7$代入$x^{2}+y^{2}=16(y≥0)$，得$y = \sqrt{16 - 2.7^{2}}=\sqrt{8.71}＞2.5$，故在离中心线2.7 m处，隧道高度高于货车的高度，所以货车能驶入这个隧道。

9. 设有半径为3 km的圆形村落，甲、乙两人同时从村落中心出发，甲向东前进而乙向北前进，甲离开村后不久，改变前进方向，斜着沿切于村落边界的方向前进，后来恰好与乙相遇. 设甲、乙两人的速度都一定，且其速度比为3 : 1，则甲、乙两人在何处相遇？

答案：
解 如图所示，以村落中心为坐标原点，东西方向为x轴，南北方向为y轴建立平面直角坐标系。设甲向东走到D然后转向走到C处时恰好与乙相遇，CD所在直线的方程为$\frac{x}{a}+\frac{y}{b}=1(a＞3,b＞3)$，乙的速度为v，则甲的速度为3v。依题意，有$\begin{cases}\frac{|ab|}{\sqrt{a^{2}+b^{2}}}=3\\\frac{\sqrt{a^{2}+b^{2}}+a}{3v}=\frac{b}{v}\end{cases}$，解得$\begin{cases}a = 5\\b = 3.75\end{cases}$，所以甲、乙在村落中心正北3.75 km处相遇。