《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

1. 已知A(0,0,2)，B(1,0,2)，C(0,2,0)，则点A到直线BC的距离为（ ）
A. $\frac{2\sqrt{2}}{3}$
B. 1
C. $\sqrt{2}$
D. $2\sqrt{2}$

答案： 1.A
∵A(0,0,2),B(1,0,2),C(0,2,0),
∴AB=(1,0,0),BC=(−1,2,−2),
∴点A到直线BC的距离为
　d=/$\sqrt{\frac{1}{9}}$1−　　=$\frac{2\sqrt{2}}{3}$

2. 已知平面$\alpha$的一个法向量$\boldsymbol{n}=(-2,-2,1)$，点A(-1,3,0)在平面$\alpha$内，则平面$\alpha$外的点P(-2,1,4)到平面$\alpha$的距离为（ ）
A. 10
B. 3
C. $\frac{8}{3}$
D. $\frac{10}{3}$

答案： 2.D　由题意可知→PA=(1,2,−4).设点P到平面α的距离为h,则h=$\frac{|PA.n|}{n|}$=$\frac{|−2−4−4|}{\sqrt{4+4+1}}$=$\frac{10}{3}$

3. 在三棱柱$ABC - A_1B_1C_1$中，$\overrightarrow{AB}=(0,1,-1)$，$\overrightarrow{AC}=(1,4,0)$，$\overrightarrow{AA_1}=(1,-1,4)$，则这个三棱柱的高$h=$（ ）
A. 1
B. $\frac{\sqrt{3}}{6}$
C. $\sqrt{2}$
D. $\frac{\sqrt{2}}{6}$

答案： 3.D　设平面ABC的法向量为n=(x,y,x),而AB=(0,1,−1),AC=(1,4,0),
　则{nn..AACB==o0,,即{yx−+x4y==0,0,
　不妨令y=x=1,则x=−4,故n=(−4,1,1),
　设三棱柱ABC−ABC的高为h,
　则h=$\frac{n.AA,}{|n|}$=$\frac{|−4×1+1×(−1)+1×4)}{\sqrt{18}}$=$\frac{√2}{6}$.

4. 已知平面$\alpha$的一个法向量为$\boldsymbol{n}=(-2,-2,1)$，点A(x,3,0)在平面$\alpha$内，且P(-2,1,4)到平面$\alpha$的距离为$\frac{10}{3}$，则x的值为（ ）
A. 1
B. 11
C. -1或-11
D. -21

答案： 4.C　由题意得PA=(x+2,2,−4),而P到平面α的距离d=$\frac{PA.n}{n|}$=$\frac{10}{3}$,即$\frac{|−2(x+2)−4−4|}{\sqrt{4+4+1}}$=$\frac{10}{3}$,
　解得x=−1或−11.故选C.

5. 如图，正方体$ABCD - A_1B_1C_1D_1$的棱长为1，O是底面$A_1B_1C_1D_1$的中心，则O点到平面$ABC_1D_1$的距离是（ ）

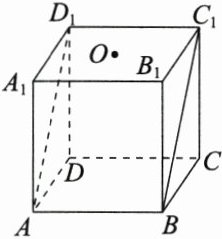
A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{4}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{3}}{2}$

答案： 5.B　以D为坐标原点,DA,DC,DD的方向分别为x,y,轴的正方向建立空间直角坐标系,则有D(0,0,1),
A(1,0,0),B(1,1,0),C(0,1,1).连接AC1,则O为
A.C的中点,
∴0($\frac{1}{2}$$\frac{1}{2}$,1),C0=($\frac{1}{2}$,一$\frac{1}{2}$,0),设平面ABC，D的法向量为n=(x,y,x),又AD=(−1,0,1),AB=(0,1,0),则有{nn..AADB==00,,
y−=x0+,z=0,取n=(1,0,1),
∴O点到平面ABCD的　　　1
　距离为d=$\frac{C,O.n}{n|}$=$\frac{2}{2}$=$\frac{\sqrt{2}}{4}$.

6.（多选）已知直线l的方向向量$\boldsymbol{n}=(1,0,-1)$，A=(2,1,-3)为直线l上一点，若点P(-1,0,-2)为直线外一点，则P到直线l上任意一点的距离可能为（ ）
A. 2
B. $\sqrt{3}$
C. $\sqrt{2}$
D. 1

答案： 6.AB　由题设条件可知,AP=(−3,−1,1),直线L的单位方向向量为n。=($\frac{\sqrt{2}}{2}$,0,−$\frac{\sqrt{2}}{2}$,所以点P到直线I的距离为d=　$\sqrt{AP²−(AP.n。)²}$=　$\sqrt{11−8}$=$\sqrt{3}$,故P 到直线1上任意一点的距离要大于或等于$\sqrt{3}$,故选AB.

7.（2024·山西阳泉期末）在空间直角坐标系Oxyz中，平面OAB的一个法向量为$\boldsymbol{n}=(2,-2,1)$. 已知点P(-1,3,2)，则点P到平面OAB的距离d = ________.

答案： 7.2
　解析　因为ōP=(−1,3,2),n=(2,−2,1),所以d=
　$\frac{n.OP}{n|}$=$\frac{|−2−6+2|}{\sqrt{4+4+1}}$=2.

8. 在棱长为2的正方体$ABCD - A_1B_1C_1D_1$中，直线AB与直线$C_1D_1$间的距离为________.

答案：
8.2√2
　解析　以D为坐标原点,建立如图所示的空间直角坐标系,则A(2,0,0),B(2,2,0),C(0,2,2),D(0,0,2),则AB=(0,2,0),DC=(0,2,0),
AD=(−2,0,2),由AB=DC,得
AB//CD,所以直线AB与直线CD
　　　　　　　　　　　　　　　　 间的距离即为点D;到直线AB的距离,
　令a=AD=(−2,0,2),u=AABB=
　$\frac{1}{2}$(0,.2,0),则a²=8,a.u=0'，所以点D到直线AB的距离为　$\sqrt{a²−(a.u)²}$=2$\sqrt{2}$二
　所以直线AB与直线CD，间的距离为2$\sqrt{2}$

9. 已知长方体$ABCD - A_1B_1C_1D_1$中，AB = 4，AD = 6，$AA_1$ = 4，M是$A_1C_1$的中点，P在线段BC上，且CP = 2，Q是$DD_1$的中点，求：
（1）M到直线PQ的距离；
（2）M到平面$AB_1P$的距离.

答案：
9.解　　如图，建立空间直角坐标系
Bxyz,
　则A(4,0,0),M(2,3,4),P(0,4,0),
　　　　　　　　　　　　　　　 Q(4,6,2),B(0,0,4).
(1)连接QM.
∵QM=(−2,−3,2),
　QP=(−4,−2,−2),
∴IQM|Q.PQ|P=$\frac{|8+6−4}{\sqrt{16+4+4}}$=$\frac{5\sqrt{6}}{6}$,
∴M到直线PQ的距离为
　　　　　　　　=　/$\sqrt{\frac{25}{6}}$17−　　=$\frac{\sqrt{462}}{6}$
(2)连接MA.设平面ABP的法向量为n=(x,y,N),则n⊥AB;,n⊥AP,
∵AB=(−4,0,4),AP=(−4,4,0),n.AB=−4x+4x=0,
∴{n.AP=−4x+4y=0,
　令x=1,则y=1,N=1,
∴n=(1,1,1).
　又MA=(2,−3,−4),
∴M到平面ABP的距离d=$\frac{MA.n}{(n)}$=$\frac{|2−3−4|}{\sqrt{3}}$
　5$\sqrt{3}$
　二30.