《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

1. 在空间四点$O$，$A$，$B$，$C$中，若$\{\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\}$是空间的一个基底，则下列说法不正确的是（ ）
A. $O$，$A$，$B$，$C$四点不共线
B. $O$，$A$，$B$，$C$四点共面，但不共线
C. $O$，$A$，$B$，$C$四点不共面
D. $O$，$A$，$B$，$C$四点中任意三点不共线

答案： 1.B故A若正四确点;共若线四,点则共向面量，O则A$\frac{.O}{OA}$，OB$\frac{.}{OB}$，OCO共C面共'面，构,不构成不基成底基,底，故B错误,C正确;若有三点共线,则这四点共面，故向量OA,OB,OC构不成基底，故D正确

2. 已知$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$是空间的一个基底，则可以与向量$\boldsymbol{p}=\boldsymbol{a}+\boldsymbol{b}$，$\boldsymbol{q}=\boldsymbol{a}-\boldsymbol{b}$构成另一个基底的向量是（ ）
A. $\boldsymbol{a}$
B. $\boldsymbol{b}$
C. $\boldsymbol{a}+2\boldsymbol{b}$
D. $\boldsymbol{a}+2\boldsymbol{c}$

答案： 2.D只有a+2c与p,q不共面,故可以与p,q构成一个基底.

3. 如图，$M$为$OA$的中点，以$\{\overrightarrow{OA},\overrightarrow{OC},\overrightarrow{OD}\}$为基底，$\overrightarrow{DM}=x\overrightarrow{OA}+y\overrightarrow{OC}+z\overrightarrow{OD}$，则有序实数组$(x,y,z)$等于（ ）

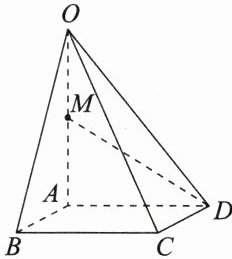
A. $(\frac{1}{2}, - 1,0)$
B. $(\frac{1}{2},0, - 1)$
C. $( - \frac{1}{2},1,0)$
D. $( - \frac{1}{2},0,1)$

答案： 3.BD忒=OM−OD=OA+00.OC−OD,所以有序实数组(x,y,权)=($\frac{1}{2}$,0,−1).故选B.

4. 已知$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$为空间的一个基底，且存在实数$x$，$y$，$z$使得$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}=\boldsymbol{0}$，则$x$，$y$，$z$的值分别为（ ）
A. $0$，$0$，$1$
B. $0$，$0$，$0$
C. $1$，$0$，$1$
D. $0$，$1$，$0$

答案： 4.B若x≠0,则a=−兰xb−xc,
∴a,b,c共面,这与{a,b,c}是基底矛盾,故x=0,同理y=0,x=0.

5. 如图所示，在三棱柱$ABC - A_{1}B_{1}C_{1}$中，$D$是四边形$BB_{1}C_{1}C$的对角线$BC_{1}$和$B_{1}C$的交点，且$\overrightarrow{AA_{1}}=\boldsymbol{a}$，$\overrightarrow{AB}=\boldsymbol{b}$，$\overrightarrow{AC}=\boldsymbol{c}$，则$\overrightarrow{A_{1}D}=$（ ）

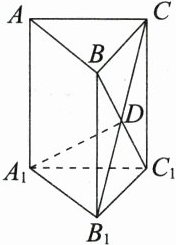
A. $\frac{1}{2}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$
B. $\frac{1}{2}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$
C. $\frac{1}{2}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}-\frac{1}{2}\boldsymbol{c}$
D. $-\frac{1}{2}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$

答案： 5.D连接A|B,则AD=$\frac{1}{2}$(AB+A，C)=$\frac{1}{2}$(AA+AB+AC)=−$\frac{1}{2}$a+$\frac{1}{2}$b+$\frac{1}{2}$c.故选D.

6. 如图，长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$AA_{1}=AB = 2$，$AD = 1$，$E$，$F$，$G$分别是$DC$，$AB$，$CC_{1}$的中点，则异面直线$A_{1}E$与$GF$所成角的余弦值是（ ）

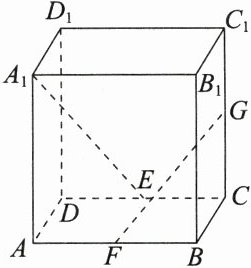
A. $0$
B. $\frac{\sqrt{3}}{3}$
C. $\frac{\sqrt{5}}{5}$
D. $\frac{\sqrt{15}}{5}$

答案： 6.A取{AA,AD,AB为空间的一个基底.根据题意，可得AE.GF=(AA+AD+DE).(GC+CB+BF)=　(−AA+AD+$\frac{1}{2}$AB).(　$\frac{1}{2}$AA−AD−$\frac{1}{2}$AB)=　$\frac{1}{2}$AA2−AD2−$\frac{1}{4}$AB2=$\frac{1}{2}$×4−1−$\frac{1}{4}$×4=0,所以AE与GF垂直,即A,E⊥GF,故AE与GF所成角的余弦值为0.

7. （2023·辽宁省实验中学期中）已知向量$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$构成空间的一个基底$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$，若$\boldsymbol{d}=3\boldsymbol{a}+4\boldsymbol{b}+\boldsymbol{c}$，且$\boldsymbol{d}=x(\boldsymbol{a}+2\boldsymbol{b})+y(\boldsymbol{b}+3\boldsymbol{c})+z(\boldsymbol{c}+\boldsymbol{a})$，则$x =$________.

答案： 7.2 解析 \(d=x(a + 2b)+y(b + 3c)+z(c + a)\) \(=(x + z)a+(2x + y)b+(3y + z)c=3a + 4b + c,\), 所以 \(\begin{cases}x + z = 3,\\2x + y = 4,\\3y+z = 1,\end{cases}\),解得 \(\begin{cases}x = 2,\\y = 0,\\z = l.\end{array}\).

8. 已知空间的一个基底$\{\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\}$，$\boldsymbol{m}=\boldsymbol{a}-\boldsymbol{b}+\boldsymbol{c}$，$\boldsymbol{n}=x\boldsymbol{a}+y\boldsymbol{b}+\boldsymbol{c}$，若$\boldsymbol{m}$与$\boldsymbol{n}$共线，则$x =$________，$y =$________.

答案： 8. \(l - l)\). 解析因为 \(m与n共线,\),所以存在实数 \(\lambda,\),使 \(m=\lambda n,\),即 \(a - b + c=\lambda xa+\lambda yb+\lambda c,\),于是有 \(\begin{array}{rcll}&\{&l=\lambda x,\\& - &l=\lambda y,\\&l=\lambda ,&\end{array}\\解得\begin{array}&\{&x = l,\\&y=-l.&\{\end{array}\\).

9. 如图，在三棱柱$ABC - A_{1}B_{1}C_{1}$中，$\angle ABC = 90^{\circ}$，$AB = BC = AA_{1}=2$，$AA_{1}\perp$平面$ABC$，$E$，$F$分别是$BB_{1}$，$A_{1}C_{1}$的中点. 求证：$AF\perp CE$.

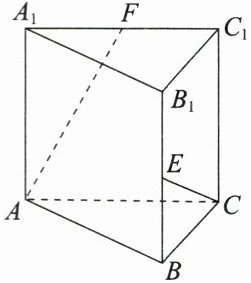
答案： 9.证明　选取{BA,BC,BB}作为空间的一个基底，设
BA=a,BC=b,BB=c.
　由已知条件和三棱柱的性质,
　得|a|=2,｜b|=2,｜c|=2,a.b=0,a.c=0,b.c=0,
AF=AA+$\frac{1}{2}$AC=AA+$\frac{1}{2}$(BC−BA)=−$\frac{1}{2}$a+$\frac{1}{2}$b+c,CE=CB+BE=−b+$\frac{1}{2}$c.因为AF.CE=
　(−$\frac{1}{2}$a+$\frac{1}{2}$b+c).(−b+$\frac{1}{2}$c)=$\frac{1}{2}$a.b−$\frac{1}{2}$b²−c.b−$\frac{1}{4}$a.c+$\frac{1}{4}$b.c+$\frac{1}{2}$c²=0,所以AF⊥CE,即
AF⊥CE.