《2024年绿色通道45分钟课时作业与单元测评数学选择性必修第一册》

1.（2024·河南新乡期末）设直线l的方向向量为$\boldsymbol{m}=(1,-1,1)$，平面$\alpha$的一个法向量为$\boldsymbol{u}=(-1,1,-1)$，则直线l与平面$\alpha$的位置关系是（ ）
A. $l\subset \alpha$
B. $l// \alpha$
C. $l\perp \alpha$
D. 不确定

答案： 1.C　因为m=一u,所以m//u,所以l⊥α.

2. 已知直线$l_1$的方向向量$\boldsymbol{a}=(1,2,-2)$，直线$l_2$的方向向量$\boldsymbol{b}=(-2,3,m)$．若$l_1\perp l_2$，则$m=$（ ）
A. 1
B. 2
C. $\frac{1}{2}$
D. 3

答案： 2.B
∵l⊥l2,
∴a.b=0,即1×(−2)+2×3+(−2)m=0,
∴m=2.

3. 两平面$\alpha,\beta$的法向量分别为$\boldsymbol{\mu}=(3,-1,z)$，$\boldsymbol{v}=(-2,-y,1)$，若$\alpha \perp \beta$，则$y + z$的值是（ ）
A. -3
B. 6
C. -6
D. -12

答案： 3.B
∵aβ,
∴μ.y=0,即−6+y+z=0,即y+x=6,故选B.

4. 已知点$A(0,1,0)$，$B(-1,0,-1)$，$C(2,1,1)$，$P(x,0,z)$，若$PA\perp$平面$ABC$，则点$P$的坐标为（ ）
A. $(1,0,-2)$
B. $(1,0,2)$
C. $(-1,0,2)$
D. $(2,0,-1)$

答案： 4.C　由题意知AB=(−1,−1,−1),AC=(2,0,1),
AP=(x,−1,N),又PA⊥平面ABC,所以AB.AP=
　　1,−　1,−1).(x,−1,x)=0,得−x+1−N=0①.$\frac{(}{AC}$.$\frac{1}{AP}$=(2,0,1).(x,−1,x)=0,得2.x+z=0　②,联立①②得x=−1,N=2,故点P的坐标为(−1,0,2).

5.（2023·山东威海期末）直三棱柱$ABC - A_1B_1C_1$中，$AA_1 = AB = AC = 1$，$AB\perp AC$，$N$是$BC$的中点，$\overrightarrow{A_1P}=\lambda \overrightarrow{A_1B_1}$，$\overrightarrow{C_1C}=3\overrightarrow{C_1M}$，若$PN\perp BM$，则$\lambda =$（ ）
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{3}{4}$

答案：
5.C　建立如图所示的空间直角坐标系.
　由题意,知B(1,0,1),M(0,,1,$\frac{1}{3}$),
　P(λ,0,0),N($\frac{1}{2}$,$\frac{1}{2}$,1),则PN=
　　　　　　　　　　　　　　　　 ($\frac{1}{2}$一λ,$\frac{1}{2}$,1),BM=(−1,1,−$\frac{2}{3}$),
∵PN⊥BM,
∴$\frac{1}{2}$−a)×(−1)+$\frac{1}{2}$×1+1×(−$\frac{2}{3}$)=0,
∴=$\frac{2}{3}$,故选C;

6. 已知平面$\alpha$的一个法向量是$\boldsymbol{a}=(\cos\theta,-\sin\theta,\sqrt{2})$，平面$\beta$的一个法向量是$\boldsymbol{b}=(\cos\theta,\sin\theta,\frac{\sqrt{2}}{2})$，若$\alpha \perp \beta$，则$\theta =$（ ）
A. $\frac{\pi}{2}$
B. $\frac{\pi}{2}+k\pi(k\in \mathbf{Z})$
C. $\frac{\pi}{2}+2k\pi(k\in \mathbf{Z})$
D. $\frac{3\pi}{2}$

答案： 6.B
∵a⊥β,
∴a.b=0,即cos²θ−sin²θ+1=0,则cos20=−1,
∴20=2kπ+π(k∈Z),则θ=kπ+$\frac{π}{2}$(k∈Z).

7. 若平面$\alpha,\beta$的法向量分别为$\boldsymbol{a}=(-1,2,4)$，$\boldsymbol{b}=(x,-1,-2)$，并且$\alpha \perp \beta$，则$x$的值为_______．

答案： 7.−10
　解析　因为α⊥β,所以它们的法向量也互相垂直，所以a.b=(−1,2,4).(x,−1,−2)=0,解得x=−10.

8. 已知$\triangle ABC$是以$\angle B$为直角的等腰直角三角形，其中$\overrightarrow{BA}=(1,m,2)$，$\overrightarrow{BC}=(2,m,n)(m,n\in \mathbf{R})$，则$m + n =$_______．

答案： 8.−1
　解析　由题意得BA.BC=O,且|BA|=|BC｜,
∴{2+$\sqrt{1+m²+4}$m²+2n==0,$\sqrt{4+m²+n²}$
∴{mn二=−0,1,
∴m+n=−1.

9. 如图，在四面体$ABOC$中，$OC\perp OA$，$OC\perp OB$，$\angle AOB = 120^{\circ}$，且$OA = OB = OC = 1$，$P$为$AC$的中点，$Q$在$AB$上且$AB = 3AQ$．证明：$PQ\perp OA$．

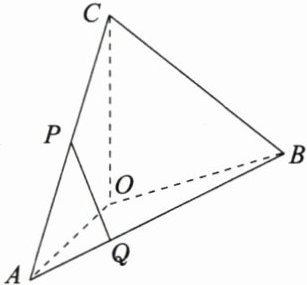
答案：
9.证明　如图,连接OP,OQ,以O为
　坐标原点，OA,OC所在直线分别为
　x轴,N轴，建立空间直角坐标系,
　则A(1,0,0),C(0,0,1)),B(−$\frac{1}{2}$,
　　　　　　　　　　　　　　 $\frac{√3}{2}$,o).
∴0A=(1,0,0),AB
　=(−$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$
(0).
∵P为AC的中点,
∴P($\frac{1}{2}$,0,$\frac{1}{2}$).ōP=($\frac{1}{2}$,0,$\frac{1}{2}$},又由已知,可得AQ=$\frac{1}{3}$AB=(−$\frac{1}{2}$,$\frac{\sqrt{3}}{6}$,0).
　又OQ=OA+AQ=($\frac{1}{2}$,$\frac{\sqrt{3}}{6}$,o),
∴PQ=OQ−OP=(0,$\frac{√3}{6}$−$\frac{1}{2}$).
∵PQ.OA=0,
∴PQ⊥$\frac{6}{OA}$,即PQ⊥OA.