《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

4. 已知□ABCD的周长为90 cm，△AOD的周长比△ABO的周长少15 cm，则AB的长为( )
A. 15 cm
B. 30 cm
C. 45 cm
D. 20 cm

答案： B 解析：
∵□ABCD的周长为90 cm，
∴AB + AD = $\frac{1}{2}×90 = 45$(cm).
∵△AOD的周长为OA + OD + AD，△ABO的周长为OA + OB + AB，OB = OD，
∴OA + OB + AB - (OA + OD + AD) = 15 cm，即AB - AD = 15 cm.
∴AB = 30 cm.

5. □ABCD的对角线相交于点O，S△AOB = 2 cm²，则S□ABCD = ______cm².

答案： 8 解析：平行四边形的两条对角线把平行四边形分成四个面积相等的三角形.

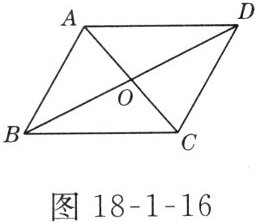
6. 如图18-1-16所示，在□ABCD中，△BCD的周长比△ABC的周长长4 cm，则OB - OC = ______.

答案： 2 cm 解析：△BCD的周长为BC + BD + CD，△ABC的周长为AB + BC + AC.
∵AB = CD，
∴(BC + BD + CD) - (AB + BC + AC) = BD - AC = 2(OB - OC) = 4 cm，
∴OB - OC = 2 cm.

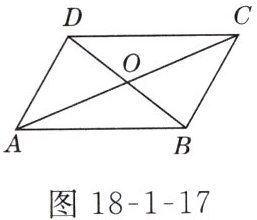
7. 如图18-1-17所示，在□ABCD中，对角线AC，BD相交于点O，若AC = 16，BD = 10，AB = 12，则△OAB的周长为______.

答案： 25

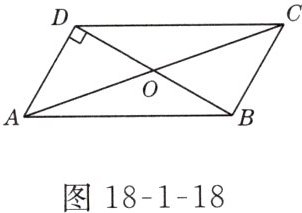
8. 如图18-1-18所示，在□ABCD中，已知∠ODA = 90°，OA = 5 cm，OB = 3 cm，求AD，AC，AB的长.

答案： 解：
∵在□ABCD中，OD = OB = 3 cm，
∴在Rt△AOD中，$AD = \sqrt{OA^{2}-OD^{2}}=\sqrt{5^{2}-3^{2}} = 4$(cm).在Rt△ABD中，$AB = \sqrt{AD^{2}+BD^{2}}=\sqrt{4^{2}+6^{2}} = 2\sqrt{13}$(cm).$AC = 2OA = 2×5 = 10$(cm).
∴AD，AC，AB的长分别是4 cm，10 cm，$2\sqrt{13}$ cm.

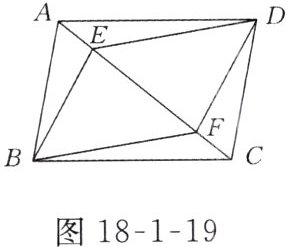
9. 如图18-1-19，已知□ABCD与□EBFD的顶点A，E，F，C在一条直线上，求证：AE = CF.

答案：
证明：如图D - 18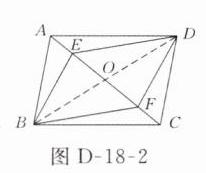 - 2所示，
连接BD，交AC于点O.
∵四边形ABCD与四边形EBFD都是平行四边形，
∴OA = OC，OE = OF，
∴OA - OE = OC - OF，即AE = CF.点拨：连接对角线，利用平行四边形的对角线互相平分，可使问题解决.

10. 如图18-1-20所示，在□ABCD中，点E，F是对角线AC上两点，且AE = CF.
求证：∠EBF = ∠FDE.

答案： 证明：
∵四边形ABCD是平行四边形，
∴AB = CD，AB//CD.
∴∠BAE = ∠DCF.又
∵AE = CF，
∴△ABE≌△CDF，
∴BE = DF.同理BF = DE.又
∵EF = FE，
∴△BEF≌△DFE，
∴∠EBF = ∠FDE.