《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

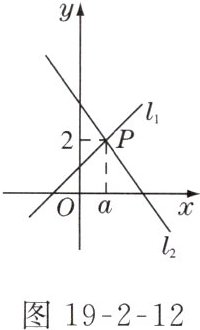
7. 如图 19 - 2 - 12 所示，直线$l_1$：$y = x + 1$与直线$l_2$：$y = mx + n$相交于点$P(a,2)$，则关于$x$，$y$的方程组$\begin{cases}y = x + 1\\y = mx + n\end{cases}$的解为________.

答案： $\begin{cases}x = 1 \\ y = 2\end{cases}$ 解析：把$P(a,2)$代入直线$y = x + 1$，得$a + 1 = 2$，所以$a = 1$，即$P(1,2)$，所以方程组$\begin{cases}y = x + 1 \\ y = mx + n\end{cases}$的解为$\begin{cases}x = 1 \\ y = 2\end{cases}$.

8. 已知一次函数$y = ax + b$（$a$，$b$是常数，$a\neq0$）中$x$与$y$的部分对应值如下表：

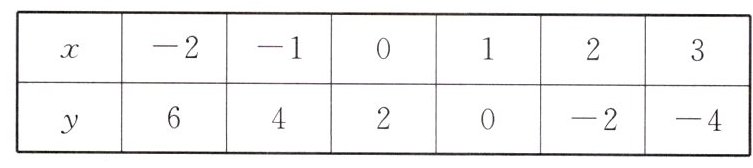
那么不等式$ax + b＞0$的解集是________.

答案： $x＜1$ 解析：本题以表格的形式给出了一次函数$y = ax + b$中$x$与$y$的部分对应值，由此可求出函数的解析式. 认真阅读表格不难发现：当$x = 1$时，$y = 0$；当$x＞1$时，$y＜0$；当$x＜1$时，$y＞0$.

9. 已知一次函数$y = 2x - 6$与$y = -x + 3$的图象交于点$P$，则点$P$的坐标为________.

答案： （3，0） 解析：由题意得方程组$\begin{cases}y = 2x - 6 \\ y = -x + 3\end{cases}$，解得$\begin{cases}x = 3 \\ y = 0\end{cases}$.
$\therefore$两函数图象的交点坐标为$P(3,0)$.

10. 已知直线$x - 2y = -k + 6$和$x + 3y = 4k + 1$，若它们的交点在第四象限内，求$k$的取值范围.

答案： 解：因为两条直线有交点，所以$\begin{cases}x - 2y = -k + 6 \\ x + 3y = 4k + 1\end{cases}$解方程组得$\begin{cases}x = k + 4 \\ y = k - 1\end{cases}$. 因为两条直线的交点在第四象限内，所以$\begin{cases}k + 4＞0 \\ k - 1＜0\end{cases}$，得$-4＜k＜1$，则$k$的取值范围是$-4＜k＜1$.

11. 用作图象的方法解方程组$\begin{cases}2x - y = 7\\3x + y = 8\end{cases}$.

答案： 分析：把方程组转化为两个一次函数，即$y = 2x - 7$和$y = -3x + 8$，然后在同一直角坐标系内画出图象，仔细观察图象，找出交点坐标即可求解.
解：由$2x - y = 7$，得$y = 2x - 7$；由$3x + y = 8$，得$y = -3x + 8$.
在同一直角坐标系内作出函数$y = 2x - 7$的图象$l_1$和$y = -3x + 8$的图象$l_2$，如图 D-19-8 所示，由图象知$l_1$与$l_2$的交点坐标为$P(3,-1)$.
故方程组$\begin{cases}2x - y = 7 \\ 3x + y = 8\end{cases}$的解为$\begin{cases}x = 3 \\ y = -1\end{cases}$.

1. 不等式的性质
性质1：不等式两边加（或减）同一个数（或式子），不等号的方向______.
性质2：不等式两边乘（或除以）同一个正数，不等号的方向______.
性质3：不等式两边乘（或除以）同一个负数，不等号的方向______.

答案： 不变 不变 改变

2. 解一元一次不等式的步骤
（1）______；（2）______；（3）______；（4）______；（5）______（注意不等号方向的改变问题）.

答案： 去分母 去括号 移项 合并同类项 系数化为1

3. 一次函数与一元一次不等式的关系
任何一元一次不等式都可以变形为______或______（a，b为常数，a≠0）的形式，解一元一次不等式可以看作当一次函数值______时，求自变量相应的取值范围.

答案： $ax + b＞0$ $ax + b＜0$ 大(小)于0