《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

5. ____________的平行四边形叫作矩形.

答案： 有一个角是直角

6. 矩形的性质
（1）矩形的四个角都是________；（2）矩形的对角线________；（3）矩形具有________的一切性质.

答案： 直角 相等 平行四边形

7. 直角三角形的性质
直角三角形斜边上的中线________________.

答案： 等于斜边的一半

8. 根据预习内容，完成下列各题.
（1）矩形具有而平行四边形不具有的性质是( )
A. 对边相等
B. 对角相等
C. 对角互补
D. 对角线互相平分
（2）在直角三角形中，若两条直角边的长分别是12和5，则斜边上的中线长为________.

答案：
(1)C
(2)$\frac{13}{2}$

1. 下列四个选项中，能够表示四边形、平行四边形、矩形的关系的是( )

答案： C 解析：矩形是特殊的平行四边形，平行四边形是特殊的四边形，故选C.

2. 在矩形ABCD中，AC与BD相交于点O，则下列说法中正确的是( )
A. AB = AD
B. BO = CO
C. ∠BAC = ∠DAC
D. AC⊥BD

答案： B

3. 若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是( )
A. 20°
B. 40°
C. 80°
D. 100°

答案：
C 解析：如图D-1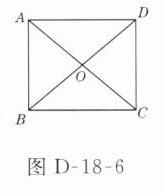8-6所示，
若$\angle DAC = 40^{\circ}$，则$\angle BAC = 50^{\circ}$.又$\because\triangle AOB,\triangle AOD$都是等腰三角形，$\therefore\angle AOB = 180^{\circ}-2\angle BAC = 80^{\circ},\angle AOD = 180^{\circ}-2\angle DAC = 100^{\circ}$，故两条对角线相交所成的锐角是$80^{\circ}$.

4. 若直角三角形斜边上的高与中线分别是5 cm和6 cm，则它的面积是________.

答案： $30\ cm^{2}$ 解析：$\because$直角三角形斜边上的中线是$6\ cm$，$\therefore$斜边长为$12\ cm$，$\therefore S_{\triangle}=\frac{1}{2}\times12\times5 = 30(cm^{2})$.

5. 若矩形一个角的平分线分矩形一边为1 cm和3 cm两部分，则这个矩形的面积为________.

答案：
$12\ cm^{2}$或$4\ cm^{2}$ 解析：由题意得，该题有两种情况：
(1)如图D-18-7所示，矩形的面积为$1\times4 = 4(cm^{2})$.
(2)如图D-18-8所示，矩形的面积为$3\times4 = 12(cm^{2})$.

6. 如图18 - 2 - 1所示，四边形ABCD是矩形，过A作AE//BD交CB的延长线于点E，猜想△ACE是怎样的三角形，并证明你的猜想.

答案： 解：$\triangle ACE$是等腰三角形.证明：$\because$四边形$ABCD$是矩形，$\therefore AD// BC,AC = BD$.又$\because AE// DB$，$\therefore$四边形$AEBD$是平行四边形，$\therefore AE = BD$，$\therefore AE = AC$，$\therefore\triangle ACE$是等腰三角形.

1. 如图18 - 2 - 2所示，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB = 60°，AB = 5，则AD的长是( )


A. 5√2
B. 5√3
C. 5
D. 10

答案： B 解析：由矩形的性质得$OA = OB$.又$\because\angle AOB = 60^{\circ}$，$\therefore\triangle AOB$是等边三角形.$\therefore AB = OB = 5$.$\therefore BD = 2OB = 2\times5 = 10$.在$Rt\triangle ABD$中，$AD = \sqrt{BD^{2}-AB^{2}}=\sqrt{10^{2}-5^{2}} = 5\sqrt{3}$.

2. 如图18 - 2 - 3所示，在矩形ABCD中，对角线AC，BD交于点O. 已知∠AOB = 60°，AC = 16，则图中长度为8的线段有( )



A. 2条
B. 4条
C. 5条
D. 6条

答案： D 解析：$\because$四边形$ABCD$为矩形，$\therefore OA = OB = OC = OD,AB = CD$. 又$\because\angle AOB = 60^{\circ}$，$\therefore\triangle AOB$为等边三角形，$\therefore AB = CD = OA = OB = OC = OD=\frac{1}{2}AC$.8. 故选D.