《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

2. 关于四边形ABCD有下列条件：①两组对边分别平行；②两组对边分别相等；③一组对边平行且相等；④对角线AC和BD相等；⑤AB//CD，AD=BC；⑥两组对角分别相等；⑦对角线AC，BD互相平分；⑧AC⊥BD. 其中可以判定四边形ABCD是平行四边形的有( )
A. 3个
B. 4个
C. 5个
D. 6个

答案： C 解析：由平行四边形的判定方法可知，①②③⑥⑦这5个条件均可判定四边形ABCD为平行四边形. 故选C.

3. 点A，B，C，D在同一平面内，从①AB//CD；②AB=CD；③BC//AD；④BC=AD这四个条件中任意选两个，能使四边形ABCD是平行四边形的选法有( )
A. 3种
B. 4种
C. 5种
D. 6种

答案： B 解析：有①②；③④；①③；②④四种选法，①②和③④运用了一组对边平行且相等，①③运用了两组对边分别平行，②④运用了两组对边分别相等来判定.

4. 一个四边形的三个内角的度数依次如下，则能判定该四边形是平行四边形的是( )
A. 88°，108°，88°
B. 88°，104°，108°
C. 88°，92°，88°
D. 88°，72°，88°

答案： C 解析：若一个四边形为平行四边形，则该四边形的对角相等，邻角互补.

5. 如图18-1-22所示，在□ABCD中，E，F分别为AD，BC边上的点，若再增加一个条件______，就可推得BE=DF.

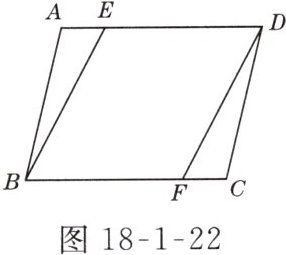
答案： BE//DF或AE = CF或DE = BF(答案不唯一)

6. 如图18-1-23所示，E，F是□ABCD的对角线BD所在直线上的两点，且BE=DF. 求证：四边形AECF是平行四边形.

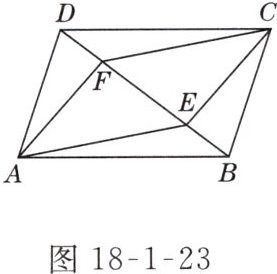
答案：
分析：由条件BE = DF，想到对角线互相平分的四边形是平行四边形，连接AC交BD于点O，如图D - 18 - 3所示，由□ABCD，知OA = OC，OB = OD，由条件BE = DF，可推出OE = OF.
证明：连接AC交BD于点O，如图D - 18 - 3所示.
∵ 四边形ABCD是平行四边形，
∴ OA = OC，OB = OD(平行四边形的对角线互相平分).
∵ BE = DF，
∴ OB - BE = OD - DF，
∴ OE = OF.
又
∵ OA = OC，
∴ 四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形).
点拨：此题也可以用三角形全等的方法来证明四边形AECF中有两组对边分别相等或者有一组对边平行且相等或者有两组对边分别平行，但都不及原证法简便. 因此，在解题时要根据已知条件合理地选择方法.

1. 下列条件中，不能判定四边形ABCD是平行四边形的是( )
A. ∠A=∠C，∠B=∠D
B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°，∠B+∠C=180°
D. ∠A+∠B=180°，∠C+∠D=180°

答案： D 解析：由选项A可得两组对角分别相等，由选项B可得两组对角分别相等，由选项C可得两组对边分别平行，故A，B，C均可证明四边形ABCD是平行四边形，而选项D中只能得出一组对边平行，故不能判定四边形ABCD是平行四边形.

2. 某广场上一个形状是平行四边形的花坛(如图18-1-24所示)，分别种有红、黄、蓝、绿、橙、紫6种颜色的花. 如果有AB//EF//DC，BC//GH//AD，那么下列说法中错误的是( )


A. 红花、绿花的种植面积一定相等
B. 紫花、橙花的种植面积一定相等
C. 红花、蓝花的种植面积一定相等
D. 蓝花、黄花的种植面积一定相等

答案： C 解析：由AB//EF//DC，BC//GH//AD，可知四边形ABCD，ADHG，BCHG都是平行四边形，另外绿红区域、黄蓝区域、紫色区域、橙色区域都是平行四边形. 由平行四边形对角线的性质可知，S绿 = S红，S黄 = S蓝，S△ABD = S△BCD，所以S紫 = S橙.

3. 如图18-1-25所示，在□ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形( )


A. OE=OF
B. DE=BF
C. ∠ADE=∠CBF
D. ∠ABE=∠CDF

答案： B 解析：选项A，由OE = OF，可以根据对角线互相平分的四边形是平行四边形来证明；C，D两选项中的角相等，可证三角形全等，得出线段相等，再进一步证线段平行，利用一组对边平行且相等的四边形是平行四边形来证明；只有选项B不能确定.

4. 点A，B，C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A，B，C，D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有( )
A. 1个
B. 2个
C. 3个
D. 4个

答案： C 解析：连接AB，BC，AC可以得到△ABC(图略)，所以以A，B，C，D四点为顶点的平行四边形有3个，即□ABCD，□ABDC和□ADBC.