《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

4. 已知一次函数$y = (6 + 3m)x + m - 4$，$y$随$x$的增大而增大，函数的图象与$y$轴的交点在$y$轴的负半轴上，则$m$的取值范围是________.

答案： $-2 ＜ m ＜ 4$ 解析：由题意得$\begin{cases}6 + 3m＞0\\m - 4＜0\end{cases}$，解得$-2 ＜ m ＜ 4$，
∴ $m$的取值范围是$-2 ＜ m ＜ 4$.

5. 若一次函数$y = 3x + b$的图象过坐标原点，则$b$的值为________.

答案： 0

6. 已知矩形的周长是8 cm，设一边长为$x$ cm，另一边长为$y$ cm.
(1)求$y$关于$x$的函数解析式，并写出自变量$x$的取值范围；
(2)在图19 - 2 - 2中作出函数图象.

答案： 解：
(1)由题意得$2(x + y)=8$，
∴ $y = 4 - x(0 ＜ x ＜ 4)$.
(2)过$(0,4)$，$(4,0)$两点的线段(不包括两端点)即为所求作函数图象，图象略.

1. 下列函数：①$y = 2x$，②$y = \frac{x}{2}$，③$y = 3x + 1$，④$y = 2x^2 + 1$. 其中一次函数的个数是（ ）
A. 4
B. 3
C. 2
D. 1

答案： B 解析：①②都是正比例函数，也都是一次函数. ③是一次函数，④不是一次函数. 故选B.

2. 如图19 - 2 - 3所示，一次函数$y = (m - 1)x - 3$的图象分别与$x$轴、$y$轴的负半轴交于点$A$，$B$，则$m$的取值范围是（ ）

A. $m＞1$
B. $m＜1$
C. $m＜0$
D. $m＞0$

答案： B 解析：
∵直线经过二、三、四象限，
∴ $m - 1＜0$，
∴ $m＜1$.

3. 一次函数$y = -2x + 4$的图象与$y$轴的交点坐标是（ ）
A. $(0,4)$
B. $(4,0)$
C. $(2,0)$
D. $(0,2)$

答案： A 解析：当$x = 0$时，$y = - 2x + 4 = - 2\times0 + 4 = 4$，
∴一次函数$y = - 2x + 4$与$y$轴的交点坐标是$(0,4)$.

4. 若正比例函数$y = kx(k\neq0)$的函数值$y$随$x$的增大而增大，则一次函数$y = x + k$的图象大致是（ ）

答案： A 解析：
∵正比例函数$y = kx(k\neq0)$的函数值$y$随$x$的增大而增大，
∴ $k＞0$，
∴一次函数$y = x + k$的图象经过一、二、三象限，故选A.

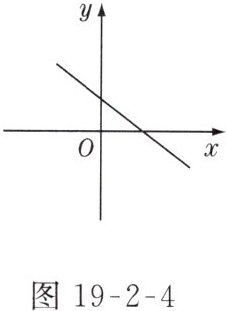
5. 已知一次函数$y = mx + n - 2$的图象如图19 - 2 - 4所示，则$m$，$n$的取值范围是（ ）

A. $m＞0$，$n＜2$
B. $m＞0$，$n＞2$
C. $m＜0$，$n＜2$
D. $m＜0$，$n＞2$

答案： D 解析：
∵一次函数$y = mx + n - 2$的图象过第一、二、四象限，
∴ $m＜0$.
∵函数的图象与$y$轴交于正半轴，
∴ $n - 2＞0$，
∴ $n＞2$，故选D.

6. 在直线$y = -3x + 2$上有两点$A(x_1,y_1)$和$B(x_2,y_2)$，若$x_1＜x_2$，则$y_1$________$y_2$.

答案： $＞$ 解析：一次函数$y = - 3x + 2$中$k = - 3＜0$，$y$随$x$的增大而减小.
∵ $x_{1}＜x_{2}$，
∴ $y_{1}＞y_{2}$.

7. 若一次函数$y = kx + 1(k$为常数，$k\neq0)$的图象经过第一、二、三象限，则$k$的取值范围是________.

答案： $k＞0$ 解析：因为直线与$y$轴交于正半轴，且过第一、二、三象限，所以$y$随$x$的增大而增大，所以$k＞0$.

8. 当$m =$________时，函数$y = (2m - 1)x^{3m - 2} + 3$是一次函数，$y$随$x$的增大而________.

答案： 1 增大

9. 已知$y + 2$与$x$成正比例，且当$x = -2$时，$y = 0$.
(1)求$y$与$x$之间的函数解析式；
(2)画出函数的图象；
(3)设点$P$在$y$轴的负半轴上，(2)中函数的图象与$x$轴、$y$轴分别交于$A$、$B$两点，且$S_{\triangle ABP} = 4$，求$P$点的坐标.

答案：
解：
(1)
∵ $y + 2$与$x$成正比例，
∴设$y + 2 = kx(k$是常数，且$k\neq0)$.
∵当$x = - 2$时，$y = 0$，
∴ $0 + 2 = k\cdot(-2)$，即$k = - 1$.
∴所求的函数解析式为$y + 2 = - x$，即$y = - x - 2$.
(2)列表如下：

描点、连线，图象如图D - 19 - 4所示.
(3)
∵函数$y = - x - 2$的图象分别交$x$轴、$y$轴于$A$、$B$两点，
∴点$A(-2,0)$，$B(0,-2)$.
设点$P$的坐标为$(0,y)$，则
$S_{\triangle ABP}=\frac{1}{2}\cdot|BP|\cdot|OA|=\frac{1}{2}\cdot|-2 - y|\cdot2 = 4$，
∴ $|-2 - y| = 4$.
∴ $y_{1} = - 6$，$y_{2} = 2$.
又
∵点$P$在$y$轴负半轴上，
∴点$P$的坐标为$(0,-6)$.