《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

3. 直角三角形两锐角的度数分别为x，y，其关系式为______.

答案： $y = 90 - x(0＜x＜90)$ 解析：直角三角形的两锐角互余.

4. 小明的父母出去散步，从家走了20 min到一个离家900 m的报亭，母亲随即按原速度返回家.父亲在报亭看了10 min报纸后，用15 min返回家.则表示父亲、母亲离家距离与时间之间的关系的图象分别是图19-1-13中的______（只需填写序号）.

答案： ④② 解析：父亲在报亭有停留只能是①或④，再根据父亲在报亭看了10 min报纸，用15 min回家，所以选④；母亲没有在报亭停留只能选②③，又因为母亲按原速返回，所以选②.

5. 甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150 m时，乙停下来等候甲，两人相遇后乙又继续以原来的速度跑向体育馆.如图19-1-14是甲、乙两人在跑步的全过程中经过的路程y(m)与甲出发的时间x(s)的函数图象.
（1）在跑步的全过程中，甲共跑了______m，甲的速度为______m/s.
（2）乙跑步的速度是多少？乙在途中等候甲用了多长时间？
（3）甲出发多长时间第一次与乙相遇？此时乙跑了多少米？

答案： 分析：观察图象，甲共跑了900 m，用时600 s，则甲的速度为$\frac{900}{600}=1.5(m/s)$，则$y_{甲}=1.5x$. 当$x = 500 s$时，$y_{甲}=750(m)$，则乙60 s跑了150 m，故乙的速度为2.5 m/s. 当甲跑了600 m时，乙跑了750 m，此时乙等候时间为$\frac{150}{1.5}=100(s)$. 求出直线AB与直线OC的交点坐标可知甲与乙第一次相遇的时间与乙跑的路程.
解：（1）900 1.5
（2）$\because y_{甲}=1.5x$，当$x = 500$时，$y_{甲}=750$，$\therefore a = 750$. $\therefore C(500,750)$.
则乙跑步的速度为$\frac{900 - 750}{560 - 500}=2.5(m/s)$.
甲跑150 m的时间也就是乙在途中等候甲的时间，为$\frac{150}{1.5}=100(s)$.
答：乙跑步的速度为2.5 m/s，乙在途中等候甲用了100 s.
（3）当$y_{甲}=150$时，$x = 100$，则$A(100,0)$，$B(400,750)$.
当$100\leq x\leq400$时，设$y_{乙}=kx + b$，
则$\begin{cases}100k + b = 0\\400k + b = 750\end{cases}$，
解得$\begin{cases}k = 2.5\\b = - 250\end{cases}$.
故$y_{乙}=2.5x - 250$.
当$y_{甲}=y_{乙}$时，$1.5x = 2.5x - 250$，解得$x = 250$.
则乙跑了150 s，所跑路程为$150×2.5 = 375(m)$.
答：甲出发250 s第一次与乙相遇，此时乙跑了375 m.

1. 一家电信公司给顾客提供两种上网收费方式：方式A以0.1元/min的价格按上网所用时间计费；方式B除月基本费20元外，再以0.05元/min的价格按上网所用时间计费.若上网所用时间为x min，收费为y元，如图19-1-15所示，在同一直角坐标系中分别描述了两种计费方式的函数的图象，有下列结论：
①图象甲描述的是方式A；
②图象乙描述的是方式B；
③当上网所用时间为500 min时，选择方式B省钱.
其中，正确结论的个数是（ ）

A. 3
B. 2
C. 1
D. 0

答案： A 解析：很明显①②正确；因为当$x＞400$时，乙的图象位于甲的图象下方，所以③正确.

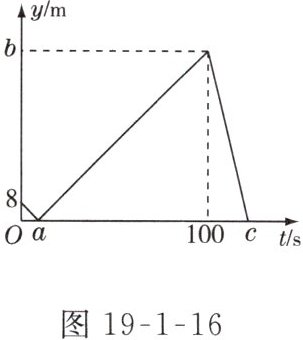
2. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m，先到终点的人原地休息，已知甲先出发2 s，在跑步过程中，甲、乙两人间的距离y(m)与乙出发的时间t(s)之间的关系如图19-1-16所示，给出以下结论：
①a=8；
②b=92；
③c=123.其中正确的是（ ）

A. ①②③
B. ①②
C. ①③
D. ②③

答案： A 解析：乙出发时甲跑了2 s，相距8 m，所以甲的速度为4 m/s，100 s后乙开始休息，所以乙的速度是$500÷100 = 5(m/s)$，$a$ s后甲、乙相遇，所以$a=\frac{8}{5 - 4}=8$，故①正确. 100 s后乙到达终点，甲跑了$4×(100 + 2)=408(m)$，所以$b = 500 - 408 = 92$，②正确. 又因为甲到终点一共耗时$500÷4 = 125(s)$，所以$c = 125 - 2 = 123$，③正确. 故选A.