《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

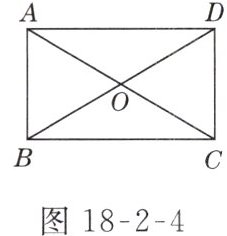
3. 如图18 - 2 - 4所示，在矩形ABCD中，AB＜BC，对角线AC，BD相交于点O，则图中的等腰三角形有( )


A. 2个
B. 4个
C. 6个
D. 8个

答案： B 解析：因为矩形的对角线相等且互相平分，所以图中的等腰三角形有$\triangle AOB$，$\triangle BOC,\triangle COD$和$\triangle AOD$，共$4$个.

4. 如图18 - 2 - 5所示，在矩形纸片ABCD中，AB = 6 cm，BC = 8 cm. 现将其沿EF对折，使得点C与点A重合，则AF的长为( )

A. 25/8 cm
B. 25/4 cm
C. 25/2 cm
D. 8 cm

答案： B 解析：由翻折得，$DF = D'F$.设$AF = x\ cm$，则$DF = D'F=(8 - x)cm$.在$Rt\triangle AFD'$中，$\because AD' = AB = 6\ cm$，$\therefore(8 - x)^{2}+6^{2}=x^{2}$.解得$x=\frac{25}{4}$，故选B.

5. 已知一个直角三角形的周长是4 + √26，斜边上的中线长是2，则这个三角形的面积是( )
A. 5
B. 5/2
C. 5/4
D. 1

答案： B 解析：设该直角三角形的两直角边长分别为$a,b$. $\because$斜边上的中线长为$2$，$\therefore$斜边长为$4$，$\therefore a + b + 4 = 4+\sqrt{26}$，$\therefore a + b=\sqrt{26}$，$\therefore(a + b)^{2}=26$，即$a^{2}+b^{2}+2ab = 26$. $\because a^{2}+b^{2}=16$，$\therefore ab = 5$，$\therefore S_{\triangle}=\frac{1}{2}ab=\frac{5}{2}$.

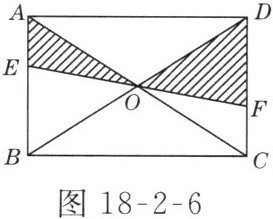
6. 如图18 - 2 - 6所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于E，F，那么阴影部分的面积是矩形面积的( )

A. 1/5
B. 1/4
C. 1/3
D. 3/10

答案： B 解析：易得$\triangle AOE\cong\triangle COF$，故$S_{阴影}=S_{\triangle COD}=\frac{1}{4}S_{矩形}$.

7. 如图18 - 2 - 7所示，已知l//m，矩形ABCD的顶点B在直线m上，且∠1 = 65°，则∠α = ________.

答案：
$25^{\circ}$ 解析：如图D-18-9所示，
过点$C$作$CE// l$. $\because l// m$，$\therefore l// m// CE$，$\therefore\angle DCE=\angle 1 = 65^{\circ}$.又$\because$四边形$ABCD$是矩形，$\therefore\angle DCB = 90^{\circ}$，$\therefore\angle ECB = 90^{\circ}-\angle DCE = 90^{\circ}-65^{\circ}=25^{\circ}$.又$\because CE// m$，$\therefore\angle\alpha=\angle ECB = 25^{\circ}$.

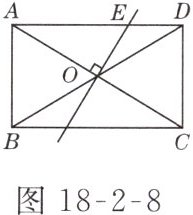
8. 如图18 - 2 - 8所示，在矩形ABCD中，AB = 3，BC = 5. 过对角线交点O作OE⊥AC，交AD于点E，则AE的长是________.

答案：
3.4 解析：连接$EC$，如图D-18-10所示.
因为$OA = OC$，$OE\perp AC$，所以$AE = EC$. 设$AE = x$，则$ED = 5 - x$.在$Rt\triangle CDE$中，根据勾股定理得$(5 - x)^{2}+3^{2}=x^{2}$，解得$x = 3.4$.

9. 在矩形ABCD中，AB = 3，BC = 4，BE⊥AC于点E，则BE = ________.

答案： $\frac{12}{5}$ 解析：在矩形$ABCD$中，$AC=\sqrt{AB^{2}+BC^{2}} = 5$. $\because S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}AC\cdot BE$，$\therefore BE=\frac{AB\cdot BC}{AC}=\frac{3\times4}{5}=\frac{12}{5}$.

10. 如图18 - 2 - 9所示，矩形ABCD沿AE折叠，使D点落在BC边上的F点处. 已知∠BAF = 58°，则∠DAE的度数是________.

答案： $16^{\circ}$ 解析：$\because\angle DAF = 90^{\circ}-\angle BAF = 90^{\circ}-58^{\circ}=32^{\circ}$，$\therefore\angle DAE=\frac{1}{2}\angle DAF = 16^{\circ}$.

11. 如图18 - 2 - 10所示，BD，CE是△ABC的高，G，F分别是BC，DE的中点. 求证：GF⊥DE.

答案：
证明：连接$EG,DG$，如图D-18-11所示.$\because CE$是$AB$边上的高，$\therefore CE\perp AB$.$\because$在$Rt\triangle CEB$中，$G$是$BC$的中点，$\therefore EG=\frac{1}{2}BC$.同理$DG=\frac{1}{2}BC$.$\therefore EG = DG$.又$\because F$是$ED$的中点，$\therefore FG\perp DE$.方法：在直角三角形中，遇斜边中点常作斜边上的中线，从而利用直角三角形斜边中线的性质解决问题.

12. 如图18 - 2 - 11所示，在矩形ABCD中，AC与BD相交于点O，BE⊥AC于点E，CF⊥BD于点F. 求证：BE = CF.

答案： 证明：在矩形$ABCD$中，$\because BO=\frac{1}{2}BD,CO=\frac{1}{2}AC,AC = BD$，$\therefore BO = CO$.$\because BE\perp AC,CF\perp BD$，$\therefore\angle BEO=\angle CFO = 90^{\circ}$.又$\because\angle EOB=\angle FOC$，$\therefore\triangle EOB\cong\triangle FOC(AAS)$，$\therefore BE = CF$.