《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

9. 如图17-2-4所示，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

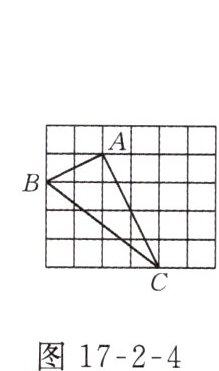
(1)画线段AD//BC，且使AD = BC，连接CD；
(2)线段AC的长为________，CD的长为________，AD的长为________；
(3)△ACD为________三角形，四边形ABCD的面积为________.

答案：
解：
(1)如图 D - 17 - 8 所示。
(2)$2\sqrt{5}$ $\sqrt{5}$ $5$
(3)直角 $10$
点拨：
(1)画图时利用格点画图更准确。
(2)利用勾股定理，知$AC=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$，$CD = AB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$AD = BC=\sqrt{3^{2}+4^{2}} = 5$。
(3)由$AC^{2}+CD^{2}=(2\sqrt{5})^{2}+(\sqrt{5})^{2}=25$，$AD^{2}=BC^{2}=25$，得$AC^{2}+CD^{2}=AD^{2}$，即$\triangle ACD$为直角三角形。所以$S_{四边形ABCD}=AC\cdot CD = 2\sqrt{5}\times\sqrt{5}=10$。

10. 如图17-2-5所示，在△ABC中，AC = 8，BC = 6，在△ABE中，DE为AB边上的高，且DE = 12，$S_{△ABE}=60$，求∠C的度数.

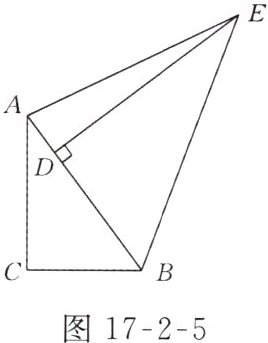
答案： 解：因为$S_{\triangle ABE}=\frac{1}{2}AB\cdot DE$，$S_{\triangle ABE}=60$，$DE = 12$，所以$60=\frac{1}{2}\times12AB$，即$AB = 10$。又因为$AC = 8$，$BC = 6$，所以$AC^{2}+BC^{2}=8^{2}+6^{2}=100=AB^{2}$。所以$\angle C = 90^{\circ}$。

11. 写出下列命题的逆命题，并判断其真假.
(1)内错角相等，两直线平行；
(2)如果两个实数的绝对值相等，那么这两个实数的平方也相等.

答案： 解：
(1)两直线平行，内错角相等。这个命题是真命题。
(2)如果两个实数的平方相等，那么这两个实数的绝对值也相等。这个命题是真命题。