第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
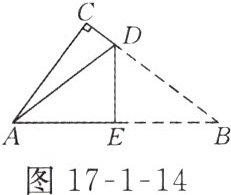
4. 如图17-1-14所示的一张直角三角形纸片,两直角边AC = 6 cm,BC = 8 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A. 4 cm
B. 5 cm
C. 6 cm
D. 10 cm

A. 4 cm
B. 5 cm
C. 6 cm
D. 10 cm
答案:
B 解析:在$Rt\triangle ABC$中,$AC = 6cm$,$BC = 8cm$,所以$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10(cm)$. 将$\triangle ABC$折叠后,点B与点A重合,则$AE = BE=\frac{1}{2}AB=\frac{1}{2}\times10 = 5(cm)$.
5. 如图17-1-15所示,在长方形纸片ABCD中,AB = 8 cm,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF = $\frac{25}{4}$ cm,则AD的长为( )

A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm

A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
答案:
C 解析:由题意,得$\triangle ABC\cong\triangle AEC$,所以$\angle FAC=\angle BAC$. 又因为ABCD为长方形纸片,所以$AB// CD$,所以$\angle BAC=\angle FCA$,所以$\angle FAC=\angle FCA$,所以$AF = CF=\frac{25}{4}cm$. 因为$DC = AB$,所以$DF = 8-\frac{25}{4}=\frac{7}{4}(cm)$. 又因为$\angle D = 90^{\circ}$,所以$AD=\sqrt{AF^{2}-DF^{2}}=\sqrt{(\frac{25}{4})^{2}-(\frac{7}{4})^{2}} = 6(cm)$.
6. 小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 2.5 m
B. 2 m
C. 2.25 m
D. 3 m
A. 2.5 m
B. 2 m
C. 2.25 m
D. 3 m
答案:
B 解析:设河水的深度为$x m$,由题意,得$(x + 0.5)^{2}=x^{2}+1.5^{2}$,解得$x = 2$.
7. 若等边三角形的边长为1,则等边三角形的高为________,面积为________.
答案:
$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{4}$ 解析:如图D - 17 - 6所示,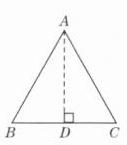
在等边三角形ABC中,过点A作$AD\perp BC$,垂足为D. 因为AD平分$\angle BAC$,所以$\angle BAD = 30^{\circ}$,$BD=\frac{1}{2}$. 在$Rt\triangle ABD$中,由勾股定理,得$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{1 - (\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$,所以$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times1\times\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{4}$ 解析:如图D - 17 - 6所示,

在等边三角形ABC中,过点A作$AD\perp BC$,垂足为D. 因为AD平分$\angle BAC$,所以$\angle BAD = 30^{\circ}$,$BD=\frac{1}{2}$. 在$Rt\triangle ABD$中,由勾股定理,得$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{1 - (\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$,所以$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times1\times\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
8. 大学毕业生小鹏现在是一名优秀的设计师,图17-1-16是他设计的一个外轮廓为长方形的机器零件平面示意图(AC,BC分别与长方形的两边平行),根据图中标出的尺寸(单位:mm),计算两圆孔中心A和B的距离为________mm.


答案:
100 解析:由AC,BC分别与长方形的两边平行,知$\triangle ABC$是以$\angle C$为直角的直角三角形. $AC = 60mm$,$BC = 80mm$,所以在$Rt\triangle ABC$中,根据勾股定理,得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{60^{2}+80^{2}} = 100(mm)$.
9. 图17-1-17是由边长为1 m的正方形地砖铺设的地面示意图,一只小猫沿图17-1-17中所示的折线从A→B→C所走的路程为________m.(结果保留根号)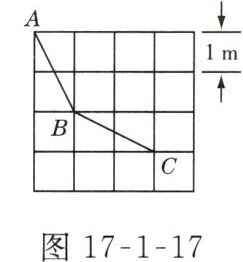

答案:
$2\sqrt{5}$ 解析:根据勾股定理,得$AB=\sqrt{1^{2}+2^{2}}=\sqrt{5}(m)$,$BC=\sqrt{1^{2}+2^{2}}=\sqrt{5}(m)$,所以$AB + BC = 2\sqrt{5}m$,即从$A\rightarrow B\rightarrow C$所走的路程为$2\sqrt{5}m$.
10. 如图17-1-18所示,在△ABC中,AB = AC,∠BAC的平分线交BC于点D,AB = 5,BC = 6,则AD = ________.


答案:
4 解析:因为$AB = AC = 5$,AD平分$\angle BAC$,所以$AD\perp BC$,$BD = CD=\frac{1}{2}BC = 3$. 在$Rt\triangle ABD$中,$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{5^{2}-3^{2}} = 4$.
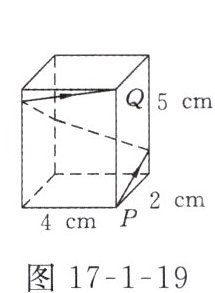
11. 如图17-1-19所示,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从点P开始经过4个侧面爬行一圈到达点Q,则蚂蚁爬行的最短路径长为________cm.

答案:
13 解析:长方体的侧面展开图如图D - 17 - 7所示.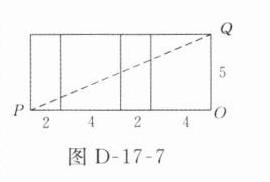
由题意,知蚂蚁爬行的最短路径长$PQ=\sqrt{PO^{2}+OQ^{2}}=\sqrt{12^{2}+5^{2}} = 13(cm)$.
13 解析:长方体的侧面展开图如图D - 17 - 7所示.

由题意,知蚂蚁爬行的最短路径长$PQ=\sqrt{PO^{2}+OQ^{2}}=\sqrt{12^{2}+5^{2}} = 13(cm)$.
12. 如图17-1-20所示,甲船以16 n mile/h的速度离开港口,向东南方向航行,乙船在同时同地向西南方向航行,已知它们离开港口1.5 h后分别到达B,A两点,且知AB = 30 n mile,问乙船每小时航行多少海里.


答案:
解:根据B在O的东南方向,A在O的西南方向,得$\angle1=\angle2 = 45^{\circ}$,
所以$\angle AOB = 90^{\circ}$,即$\triangle AOB$是直角三角形.
又$BO = 16\times1.5 = 24(n mile)$,$AB = 30n mile$,
根据勾股定理,得$AO^{2}=AB^{2}-BO^{2}=30^{2}-24^{2}=18^{2}$,
所以$AO = 18n mile$.
所以乙船的速度为$\frac{18}{1.5}=12(n mile/h)$.
答:乙船每小时航行12 n mile.
所以$\angle AOB = 90^{\circ}$,即$\triangle AOB$是直角三角形.
又$BO = 16\times1.5 = 24(n mile)$,$AB = 30n mile$,
根据勾股定理,得$AO^{2}=AB^{2}-BO^{2}=30^{2}-24^{2}=18^{2}$,
所以$AO = 18n mile$.
所以乙船的速度为$\frac{18}{1.5}=12(n mile/h)$.
答:乙船每小时航行12 n mile.
查看更多完整答案,请扫码查看


