《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

9. 已知一次函数$y = kx + b$的图象经过点$(3,-3)$，且与直线$y = 4x - 3$的交点在$x$轴上；
（1）求这个一次函数的解析式.
（2）此函数的图象经过哪几个象限？
（3）求此函数的图象与坐标轴围成的三角形的面积.

答案： 解：（1）对于一次函数$y = 4x - 3$，当$y = 0$时，$x = \frac{3}{4}$.
∴ 它的图像与$x$轴的交点为$(\frac{3}{4},0)$，
∴ 直线$y = kx + b$经过点$(3,-3)$和点$(\frac{3}{4},0)$，
∴ $\begin{cases}3k + b = -3\\\frac{3}{4}k + b = 0\end{cases}$，解得$\begin{cases}k = -\frac{4}{3}\\b = 1\end{cases}$.
∴ 一次函数的解析式为$y = -\frac{4}{3}x + 1$.
（2）
∵ $k = -\frac{4}{3} ＜ 0$，$b = 1 ＞ 0$，
∴ 一次函数$y = -\frac{4}{3}x + 1$的图象经过第一、二、四象限.
（3）
∵ 当$x = 0$时，$y = 1$；当$y = 0$时，$x = \frac{3}{4}$，
∴ 该一次函数的图象与坐标轴围成的三角形的面积为$S = \frac{1}{2}×1×\frac{3}{4} = \frac{3}{8}$.

10. 为了保护学生的视力，课桌椅的高度都是按一定比例配套设计的. 假设课桌的高度为$y$ cm，椅子的高度（不含靠背）为$x$ cm，且$y$是$x$的一次函数. 下表列出了两套符合条件的课桌椅的高度：

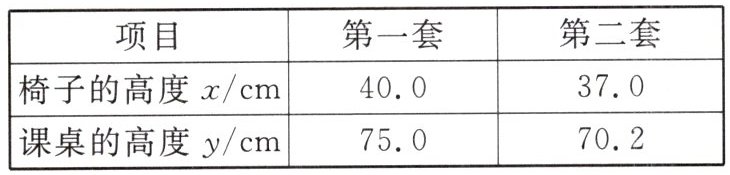
（1）请确定$y$关于$x$的函数解析式.
（2）现有一把高42.0 cm的椅子和一张高78.2 cm的课桌，它们是否配套？请通过计算说明理由.

答案： 解：（1）由题意可设函数的解析式为$y = kx + b(k\neq0)$.
将$x = 40.0$，$y = 75.0$；$x = 37.0$，$y = 70.2$代入上式，得方程组$\begin{cases}75.0 = 40.0k + b\\70.2 = 37.0k + b\end{cases}$，解得$\begin{cases}k = 1.6\\b = 11.0\end{cases}$.
所以$y$关于$x$的函数解析式为$y = 1.6x + 11.0$.
（2）配套. 理由如下：把$x = 42.0$代入函数解析式，得$y = 1.6×42.0 + 11.0 = 78.2$，与课桌的实际高度相等.
所以一把高$42.0\ cm$的椅子和一张高$78.2\ cm$的课桌刚好配套.

1. 一般地，形如____________________的函数，叫作一次函数.

答案： $y = kx + b$（$k$，$b$是常数，$k\neq0$）