《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

1. 正比例函数的图象及性质

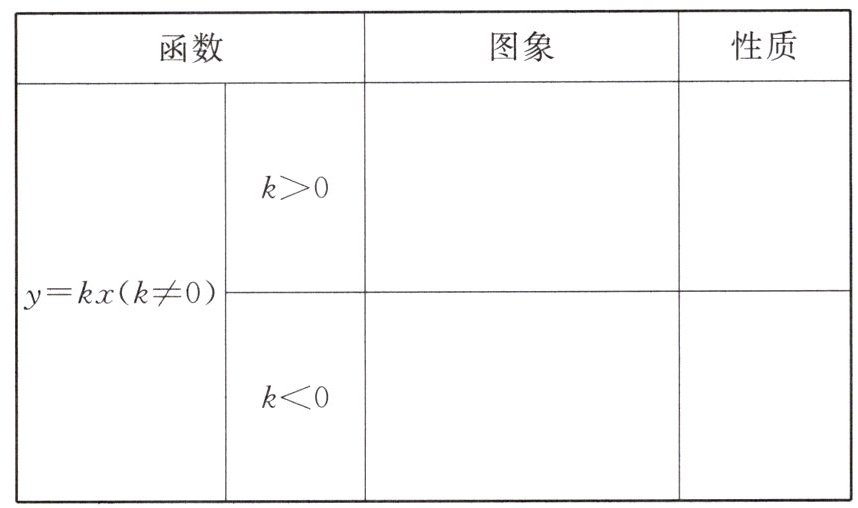
答案：

2. 描点法画函数图象的一般步骤是：
①________，②________，③________.

答案： 列表 描点 连线

3. 一般地，形如________的函数，叫作一次函数. 当$b =$________时，$y = kx + b$即$y =$________，故正比例函数是一种特殊的一次函数.

答案： $y = kx + b(k,b$是常数，$k\neq0)$ $0$ $kx$

4. 一次函数$y = kx + b(k\neq0)$的图象可以由直线$y = kx$平移________个单位长度得到（当$b＞0$时，向上平移；当$b＜0$时，向下平移）. 一次函数$y = kx + b(k\neq0)$的图象是________，我们称它为________.

答案： $|b|$ 一条直线 直线$y = kx + b$

5. 一次函数$y = kx + b(k,b$是常数，$k\neq0)$具有如下性质：
当$k＞0$时，$y$随$x$的增大而________；
当$k＜0$时，$y$随$x$的增大而________.

答案： 增大 减小

6. 根据预习内容填空.
直线$y = 3x - 5$与$x$轴的交点坐标为________，与$y$轴的交点坐标为________，图象经过________象限，$y$随$x$的增大而________.

答案： $(\frac{5}{3},0)$ $(0,-5)$ 一、三、四 增大

1. 下列函数解析式中，不是一次函数的是（ ）
A. $y = -\frac{x}{5}$
B. $s = 3t + 4$
C. $y = x + 2^2$
D. $y = -\frac{1}{x}$

答案： D 解析：判断一个函数是否为一次函数，就是看该函数能否通过恒等变形，把它变成$y = kx + b(k,b$是常数，$k\neq0)$的形式. $y = -\frac{x}{5}$中，$k = -\frac{1}{5}$，$b = 0$，是正比例函数，也是一次函数；$s = 3t + 4$中，$k = 3$，$b = 4$，是一次函数；$y = x + 2^{2}$中，$k = 1$，$b = 2^{2}$，是一次函数；$y = -\frac{1}{x}$中，分母中含有未知数，不是一次函数，故选D.

2. 直线$y = x - 1$的图象经过的象限是（ ）
A. 第一、二、三象限
B. 第一、二、四象限
C. 第二、三、四象限
D. 第一、三、四象限

答案： D 解析：直线$y = x - 1$与$y$轴交于$(0,-1)$，且$k = 1＞0$，$y$随$x$的增大而增大，
∴直线$y = x - 1$的图象经过第一、三、四象限.

3. 在一次函数$y = kx + 3$中，如果当$x = 2$时，$y = -3$，那么当$x = -2$时，$y$等于（ ）
A. -1
B. -3
C. 7
D. 9

答案： D 解析：将$x = 2$，$y = - 3$代入$y = kx + 3$，解得$k = - 3$，所以当$x = - 2$时，$y = (-3)\times(-2)+3 = 9$.