第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
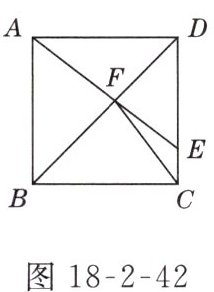
2. 如图18-2-42所示,在正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有( )
A. 1对 B. 2对 C. 3对 D. 4对

A. 1对 B. 2对 C. 3对 D. 4对
答案:
C 解析:由正方形的对称性可知△ABD≌△CBD,△AFD≌△CFD,△ABF≌△CBF,故全等三角形有 3 对.
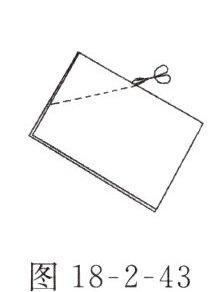
3. 如图18-2-43所示,把一张长方形纸片对折两次,然后剪下一个角,为了得到一个正方形,剪刀与折痕所成的角的度数应为( )
A. 60°
B. 30°
C. 45°
D. 90°

A. 60°
B. 30°
C. 45°
D. 90°
答案:
C 解析:由折法可知,剪得的四边形对角线垂直且互相平分,即为菱形,要想得到正方形,需有一个内角是 90°,即剪刀与折痕所成的角应为 90°÷2 = 45°,故选 C.
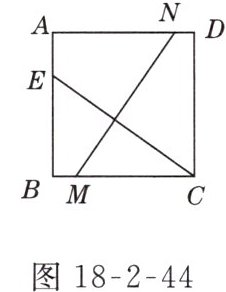
4. 如图18-2-44所示,在正方形ABCD中,CE = MN,∠MCE = 35°,那么∠ANM =( )
A. 45°
B. 50°
C. 55°
D. 60°

A. 45°
B. 50°
C. 55°
D. 60°
答案:
C 解析:过点 M 作 MF⊥AD 于点 F,如图 D-18-17 所示,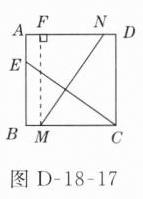
在 Rt△BEC 与 Rt△FNM 中,BC = FM,CE = MN,
∴ Rt△BEC≌Rt△FNM,图 D-18-17
∴ ∠NMF = ∠ECB = 35°,
∴ ∠ANM = 90° - ∠NMF = 90° - 35° = 55°,故选 C.
C 解析:过点 M 作 MF⊥AD 于点 F,如图 D-18-17 所示,

在 Rt△BEC 与 Rt△FNM 中,BC = FM,CE = MN,
∴ Rt△BEC≌Rt△FNM,图 D-18-17
∴ ∠NMF = ∠ECB = 35°,
∴ ∠ANM = 90° - ∠NMF = 90° - 35° = 55°,故选 C.
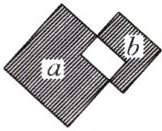
5. 如图18-2-45所示,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a - b)等于( )
A. 7
B. 6
C. 5
D. 4

A. 7
B. 6
C. 5
D. 4
答案:
A 解析:观察图形,矩形面积 = 16 - a = 9 - b,所以 a - b = 16 - 9 = 7.
6. 如图18-2-46所示,从边长为(a + 4)cm的正方形纸片中剪去一个边长为(a + 1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
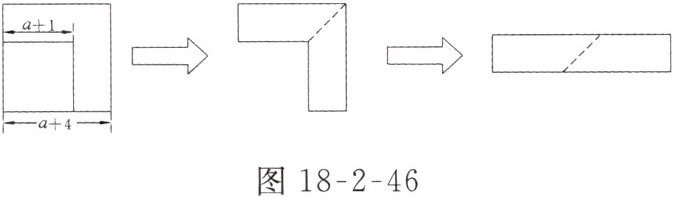
A. (2a² + 5a)cm²
B. (3a + 15)cm²
C. (6a + 9)cm²
D. (6a + 15)cm²

A. (2a² + 5a)cm²
B. (3a + 15)cm²
C. (6a + 9)cm²
D. (6a + 15)cm²
答案:
D
7. 如图18-2-47所示,E为正方形ABCD外一点,若△ADE为等边三角形,则∠AEB = __________.
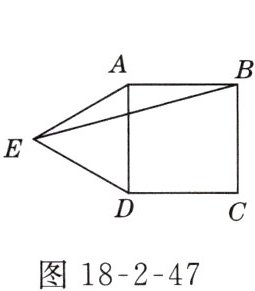

答案:
15° 解析:
∵ 四边形 ABCD 为正方形,△ADE 为等边三角形,
∴ ∠DAB = 90°,∠EAD = 60°,AB = AE,
∴ ∠EAB = 60° + 90° = 150°,∠AEB = ∠ABE,
∴ ∠AEB = 1/2(180° - 150°) = 15°.
∵ 四边形 ABCD 为正方形,△ADE 为等边三角形,
∴ ∠DAB = 90°,∠EAD = 60°,AB = AE,
∴ ∠EAB = 60° + 90° = 150°,∠AEB = ∠ABE,
∴ ∠AEB = 1/2(180° - 150°) = 15°.
8. 如图18-2-48所示,正方形ABCD的对角线长为8√2,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF + EG = __________.


答案:
4√2 解析:由正方形的性质得△BEG 是等腰直角三角形,故 EG = BG. 又
∵ EF⊥AC,EG⊥BD,AC⊥BD,
∴ 四边形 EGOF 为矩形,
∴ EF = OG,
∴ EF + EG = OG + BG = BO = 1/2BD = 1/2×8√2 = 4√2.
∵ EF⊥AC,EG⊥BD,AC⊥BD,
∴ 四边形 EGOF 为矩形,
∴ EF = OG,
∴ EF + EG = OG + BG = BO = 1/2BD = 1/2×8√2 = 4√2.
9. 如图18-2-49,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD,BC于点E,F,则阴影部分的面积是__________.


答案:
1 解析:
∵ 四边形 ABCD 为正方形,
∴ OD = OB,OA = OC,AC⊥BD.
∵ DE//BC,
∴ ∠EDO = ∠FBO.又
∵ ∠DOE = ∠BOF,
∴ △DOE≌△BOF,故 S△DOE = S△BOF,
∴ S阴影 = S△DOE + S△OFC = S△BOF + S△OFC = S△BOC = 1/4S正方形ABCD = 1/4×2×2 = 1.
∵ 四边形 ABCD 为正方形,
∴ OD = OB,OA = OC,AC⊥BD.
∵ DE//BC,
∴ ∠EDO = ∠FBO.又
∵ ∠DOE = ∠BOF,
∴ △DOE≌△BOF,故 S△DOE = S△BOF,
∴ S阴影 = S△DOE + S△OFC = S△BOF + S△OFC = S△BOC = 1/4S正方形ABCD = 1/4×2×2 = 1.
10. 如图18-2-50,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别在OD,OC上,且DE = CF,连接DF,AE,AE的延长线交DF于点M.
求证:AM⊥DF.

求证:AM⊥DF.

答案:
证明:
∵ 四边形 ABCD 是正方形,
∴ AD = CD,∠ADE = 45°,∠DCF = 45°,∠ADC = 90°.在△ADE 与△DCF 中,{AD = DC,∠ADE = ∠DCF,DE = CF,
∴ △ADE≌△DCF(SAS).
∴ ∠DAE = ∠CDF.又
∵ ∠CDF + ∠ADF = 90°,
∴ ∠DAE + ∠ADF = 90°.
∴ ∠AMD = 90°,即 AM⊥DF.
∵ 四边形 ABCD 是正方形,
∴ AD = CD,∠ADE = 45°,∠DCF = 45°,∠ADC = 90°.在△ADE 与△DCF 中,{AD = DC,∠ADE = ∠DCF,DE = CF,
∴ △ADE≌△DCF(SAS).
∴ ∠DAE = ∠CDF.又
∵ ∠CDF + ∠ADF = 90°,
∴ ∠DAE + ∠ADF = 90°.
∴ ∠AMD = 90°,即 AM⊥DF.
11. 如图18-2-51所示,已知在△ABC中,AB = AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A = 90°,求证:四边形DFAE是正方形.

(1)求证:△BED≌△CFD;
(2)若∠A = 90°,求证:四边形DFAE是正方形.

答案:
证明:(1)
∵ DE⊥AB,DF⊥AC,
∴ ∠BED = ∠CFD = 90°.
∵ AB = AC,
∴ ∠B = ∠C.
∵ D 是 BC 边的中点,
∴ BD = CD,
∴ △BED≌△CFD.(2)
∵ DE⊥AB,DF⊥AC,
∴ ∠AED = ∠AFD = 90°.
∵ ∠A = 90°,
∴ 四边形 DFAE 是矩形.
∵ △BED≌△CFD,
∴ DE = DF.
∴ 四边形 DFAE 是正方形.
∵ DE⊥AB,DF⊥AC,
∴ ∠BED = ∠CFD = 90°.
∵ AB = AC,
∴ ∠B = ∠C.
∵ D 是 BC 边的中点,
∴ BD = CD,
∴ △BED≌△CFD.(2)
∵ DE⊥AB,DF⊥AC,
∴ ∠AED = ∠AFD = 90°.
∵ ∠A = 90°,
∴ 四边形 DFAE 是矩形.
∵ △BED≌△CFD,
∴ DE = DF.
∴ 四边形 DFAE 是正方形.
查看更多完整答案,请扫码查看


