《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

3. 某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办海产品运输业务，已知运输路程为120 km，汽车和火车的速度分别为60 km/h，100 km/h，两货运公司的收费项目及收费标准如下表所示：

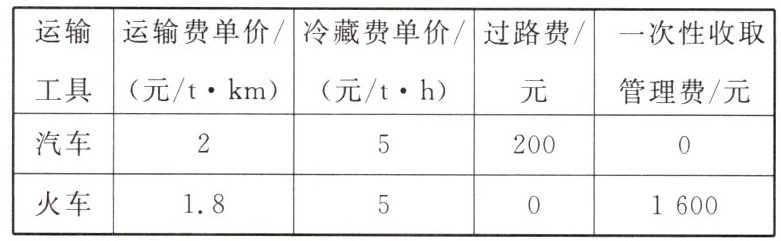
（注：“元/t·km”表示每吨货物每千米的运费，“元/t·h”表示每吨货物每小时的冷藏费）
（1）设该批发商待运的海产品有x t，汽车货运公司和铁路货运公司所要收取的费用分别为y1元和y2元，求y1和y2关于x的函数解析式；
（2）若该批发商待运的海产品不少于30 t，为节省运费，他应该选择哪个货运公司承担运输业务？

答案： 解：
(1)根据题意，得
$y_{1}=200 + 2\times120x+5\times\frac{120}{60}x = 250x + 200$，
$y_{2}=1600 + 1.8\times120x+5\times\frac{120}{100}x = 222x + 1600$.
(2)分三种情况：
①若$y_{1}＞y_{2}$，即$250x + 200＞222x + 1600$，
解得$x＞50$；
②若$y_{1}=y_{2}$，即$250x + 200 = 222x + 1600$，
解得$x = 50$；
③若$y_{1}＜y_{2}$，即$250x + 200＜222x + 1600$，
解得$x＜50$.
即当待运海产品不少于30 t，且不足50 t时，应选择汽车货运公司；
当待运海产品恰好50 t时，选择两家公司一样；
当待运海产品多于50 t时，应选择铁路货运公司.

1. A，B两家公司分别采取如下工资支付方式：A公司每月6 000元基本工资，另加销售额的2％作为奖金；B公司每月4 800元基本工资，另加销售额的4％作为奖金. 已知A，B两家公司两位销售员小李、小张1～6月份的销售额如下表：

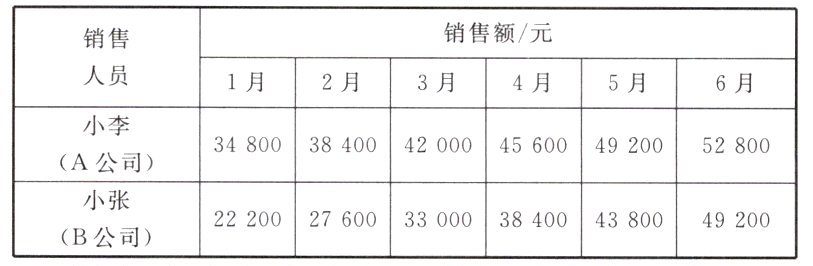
（1）请问小李与小张3月份的工资各是多少？
（2）小李1～6月份的销售额y1与月份x的函数解析式是y1 = 3 600x + 31 200，小张1～6月份的销售额y2也是月份x的一次函数，请求出y2与x的函数解析式；
（3）如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资？

答案： 解：
(1)小李3月份的工资为$6000 + 2\%\times42000 = 6840$（元），
小张3月份的工资为$4800 + 4\%\times33000 = 6120$（元）.
(2)设$y_{2}=kx + b$，取表中的两对数(1，22200)、(2，27600)代入上式，得
$\begin{cases}22200 = k + b\\27600 = 2k + b\end{cases}$，解得$\begin{cases}k = 5400\\b = 16800\end{cases}$
即$y_{2}=5400x + 16800$.
(3)小李的工资$w_{1}=6000 + 2\%(3600x + 31200)=72x + 6624$，小张的工资$w_{2}=4800 + 4\%(5400x + 16800)=216x + 5472$. 当小张的工资高于小李的工资时，即$216x + 5472＞72x + 6624$，解得$x＞8$. 即从9月份开始小张的工资高于小李的工资.

2. 某校准备组织290名学生进行野外考察活动，行李共有100件. 学校计划租用甲、乙两种型号的汽车共8辆. 经了解，甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李.
（1）设租用甲种汽车x辆，请你帮助学校设计所有可能的租车方案；
（2）如果甲、乙两种汽车每辆的租车费用分别为2 000元、1 800元，请你选择最省钱的一种租车方案.

答案： 解：
(1)由于租用甲种汽车$x$辆，则租用乙种汽车$(8 - x)$辆.
由题意，得$\begin{cases}40x + 30(8 - x)\geqslant290\\10x + 20(8 - x)\geqslant100\end{cases}$，解得$5\leqslant x\leqslant6$.
即共有两种租车方案：
第一种方案是租用甲种汽车5辆，乙种汽车3辆；
第二种方案是租用甲种汽车6辆，乙种汽车2辆.
(2)第一种租车方案的费用为$5\times2000 + 3\times1800 = 15400$（元），
第二种租车方案的费用为$6\times2000 + 2\times1800 = 15600$（元）.
由$15400＜15600$，知第一种租车方案最省钱.