第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
3.已知菱形的周长是40cm,两对角线长度之比为3:4,则这两条对角线的长度分别是( )
A.6 cm,8 cm
B.3 cm,4 cm
C.12 cm,16 cm
D.24 cm,32 cm
答案:
C 解析:菱形的周长是40 cm,所以菱形的边长为10 cm. 两条对角线的一半与菱形的一边构成直角三角形,又因为菱形两对角线一半的长度之比为3∶4,所以两条对角线一半的长度分别是6 cm,8 cm,故两条对角线的长度分别是12 cm,16 cm.
4.已知菱形ABCD的两条对角线相交于点O,若AB=6,∠BDC=30°,则菱形的面积为 ___________
答案:
18$\sqrt{3}$ 解析:如图D - 18 - 13所示,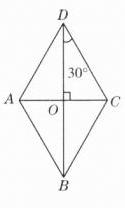
在菱形ABCD中,DC = AB = 6,∠BDC = 30°,
∴在Rt△DOC中,OC = 3,
∴OD = $\sqrt{DC^{2}-OC^{2}}$ = 3$\sqrt{3}$,
∴$S_{菱形ABCD} = 4S_{△DOC}$ = 4×$\frac{1}{2}$×3×3$\sqrt{3}$ = 18$\sqrt{3}$.
18$\sqrt{3}$ 解析:如图D - 18 - 13所示,

在菱形ABCD中,DC = AB = 6,∠BDC = 30°,
∴在Rt△DOC中,OC = 3,
∴OD = $\sqrt{DC^{2}-OC^{2}}$ = 3$\sqrt{3}$,
∴$S_{菱形ABCD} = 4S_{△DOC}$ = 4×$\frac{1}{2}$×3×3$\sqrt{3}$ = 18$\sqrt{3}$.
5.如图18-2-20所示,在菱形ABCD中,∠A=60°,对角线BD=8,则菱形ABCD的周长为___________

答案:
32 解析:在菱形ABCD中,
∵∠A = 60°,
∴△ABD是等边三角形,
∴AB = BD = 8,
∴菱形ABCD的周长为4×8 = 32.
∵∠A = 60°,
∴△ABD是等边三角形,
∴AB = BD = 8,
∴菱形ABCD的周长为4×8 = 32.
6.如图18-2-21所示,已知菱形ABCD 的边长为2cm,∠BAD=120',对角线AC和BD相交于点O,求这个菱形的面积

答案:
分析:选取Rt△AOB,利用对角线的性质求出各角,由“30°角所对的直角边等于斜边的一半”及勾股定理求出对角线的长后,用公式S = $\frac{1}{2}$AC·BD求面积. 也可以过点A作BC边上的高线,利用直角三角形的性质和勾股定理求高,进而求面积. 解法1:因为四边形ABCD是菱形, 所以AC⊥BD,AO = $\frac{1}{2}$AC,BO = $\frac{1}{2}$BD, ∠BAO = $\frac{1}{2}$∠BAD = $\frac{1}{2}$×120° = 60°. 在Rt△AOB中,∠ABO = 90° - ∠BAO = 30°, 所以AO = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1(cm), 所以BO = $\sqrt{AB^{2}-AO^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$(cm). 因为AO = $\frac{1}{2}$AC,BO = $\frac{1}{2}$BD, 所以AC = 2AO = 2 cm,BD = 2BO = 2$\sqrt{3}$ cm, 所以$S_{菱形ABCD}$ = $\frac{1}{2}$AC·BD = 2$\sqrt{3}$(cm$^{2})$. 解法2:如图D - 18 - 14所示,过点A作AH⊥BC,垂足为H. 因为∠BAD = 120°,四边形ABCD是菱形,所以∠BAH = 120° - 90° = 30°, 所以BH = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1(cm), 所以AH = $\sqrt{AB^{2}-BH^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$(cm), 所以$S_{菱形ABCD}$ = BC·AH = 2$\sqrt{3}$($cm^{2}$).
分析:选取Rt△AOB,利用对角线的性质求出各角,由“30°角所对的直角边等于斜边的一半”及勾股定理求出对角线的长后,用公式S = $\frac{1}{2}$AC·BD求面积. 也可以过点A作BC边上的高线,利用直角三角形的性质和勾股定理求高,进而求面积. 解法1:因为四边形ABCD是菱形, 所以AC⊥BD,AO = $\frac{1}{2}$AC,BO = $\frac{1}{2}$BD, ∠BAO = $\frac{1}{2}$∠BAD = $\frac{1}{2}$×120° = 60°. 在Rt△AOB中,∠ABO = 90° - ∠BAO = 30°, 所以AO = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1(cm), 所以BO = $\sqrt{AB^{2}-AO^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$(cm). 因为AO = $\frac{1}{2}$AC,BO = $\frac{1}{2}$BD, 所以AC = 2AO = 2 cm,BD = 2BO = 2$\sqrt{3}$ cm, 所以$S_{菱形ABCD}$ = $\frac{1}{2}$AC·BD = 2$\sqrt{3}$(cm$^{2})$. 解法2:如图D - 18 - 14所示,过点A作AH⊥BC,垂足为H. 因为∠BAD = 120°,四边形ABCD是菱形,所以∠BAH = 120° - 90° = 30°, 所以BH = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1(cm), 所以AH = $\sqrt{AB^{2}-BH^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$(cm), 所以$S_{菱形ABCD}$ = BC·AH = 2$\sqrt{3}$($cm^{2}$).

1. 若菱形的周长为8 cm,高为1 cm,则菱形两邻角的度数比为( )
A. 3∶1
B. 4∶1
C. 5∶1
D. 6∶1
A. 3∶1
B. 4∶1
C. 5∶1
D. 6∶1
答案:
C
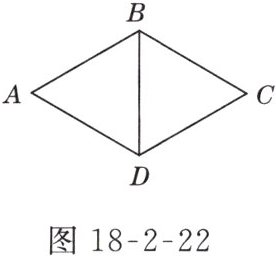
2. 如图18-2-22所示,菱形ABCD的周长是16,∠A = 60°,则对角线BD的长为( )
A. 2
B. $\sqrt{3}$
C. 4
D. 3

A. 2
B. $\sqrt{3}$
C. 4
D. 3
答案:
C
3. 如图18-2-23所示,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF = 2,那么菱形ABCD的周长是( )

A. 4
B. 8
C. 12
D. 16

A. 4
B. 8
C. 12
D. 16
答案:
D
4. 如图18-2-24所示,在菱形ABCD中,对角线AC与BD相交于点O,OE//DC且交BC于点E,AD = 6 cm,则OE的长为( )

A. 6 cm
B. 4 cm
C. 3 cm
D. 2 cm

A. 6 cm
B. 4 cm
C. 3 cm
D. 2 cm
答案:
C
5. 如图18-2-25所示,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E. 若∠ADC = 130°,则∠AOE的大小为( )

A. 75°
B. 65°
C. 55°
D. 50°

A. 75°
B. 65°
C. 55°
D. 50°
答案:
B
6. 如图18-2-26所示,在菱形ABCD中,∠B = 60°,AB = 2 cm,E,F分别是BC,CD的中点,连接AE,EF,AF,则△AEF的周长为( )

A. $2\sqrt{3}$ cm
B. $3\sqrt{3}$ cm
C. $4\sqrt{3}$ cm
D. 3 cm

A. $2\sqrt{3}$ cm
B. $3\sqrt{3}$ cm
C. $4\sqrt{3}$ cm
D. 3 cm
答案:
B
7. 已知菱形的周长为40 cm,两条对角线长度之比为3∶4,则菱形的面积为______.
答案:
96 cm$^{2}$
8. 如图18-2-27所示,在菱形ABCD中,∠A = 60°,E,F分别是AB,AD的中点,若EF = 2,则菱形ABCD的边长是______.


答案:
4
9. 在菱形ABCD中,∠ABC = 120°,AB = 10 cm,则AC = ______,BD = ______.
答案:
10$\sqrt{3}$ cm 10 cm
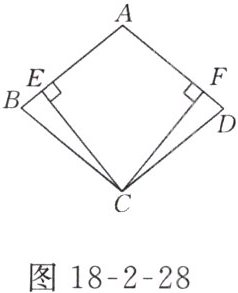
10. 如图18-2-28所示,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE = AF.

答案:
分析:要证明AE = AF,先证△ACE≌△ACF或△BCE≌△DCF.
证法1:如图D - 18 - 15所示,连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC = ∠DAC.
在△ACE和△ACF中,
∠AEC = ∠AFC = 90°,∠BAC = ∠DAC,AC = AC,
∴△ACE≌△ACF(AAS),
∴AE = AF.
证法2:
∵四边形ABCD是菱形,
∴BC = DC = AD = AB,∠B = ∠D.
又∠BEC = ∠DFC = 90°,
∴△BCE≌△DCF(AAS),
∴BE = DF,
∴AE = AF.
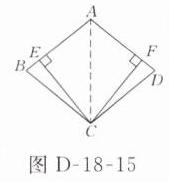
分析:要证明AE = AF,先证△ACE≌△ACF或△BCE≌△DCF.
证法1:如图D - 18 - 15所示,连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC = ∠DAC.
在△ACE和△ACF中,
∠AEC = ∠AFC = 90°,∠BAC = ∠DAC,AC = AC,
∴△ACE≌△ACF(AAS),
∴AE = AF.
证法2:
∵四边形ABCD是菱形,
∴BC = DC = AD = AB,∠B = ∠D.
又∠BEC = ∠DFC = 90°,
∴△BCE≌△DCF(AAS),
∴BE = DF,
∴AE = AF.

查看更多完整答案,请扫码查看


