《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

1. 如图17-1-9所示，P是第一象限的角平分线上一点，且OP = 2，则点P的坐标是( )


A. (2，2)
B. ($\sqrt{2}$，$\sqrt{2}$)
C. (2，$\sqrt{2}$)
D. ($\sqrt{2}$，2)

答案：
B 解析：如图D - 1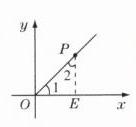7 - 1所示，
过点P向x轴作垂线，垂足为E. 因为点P在第一象限的角平分线上，所以$\angle1 = 45^{\circ}$. 易知△OPE是等腰直角三角形，即$OE = PE$. 设$PE = x$，则$OE = x$，故在$Rt\triangle OPE$中，由勾股定理，得$x^{2}+x^{2}=2^{2}$，解得$x = \sqrt{2}$. 所以点P的坐标是$(\sqrt{2},\sqrt{2})$，故选B.

2. 如图17-1-10所示，一架长为5 m的梯子，斜靠在一竖直的墙上，这时梯足距墙脚3 m，若梯子的顶端下滑1 m，则梯足将滑动( )

A. 0 m B. 1 m
C. 2 m D. 3 m

答案： B 解析：在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AB = 5m$，$BC = 3m$，
由勾股定理，得$AB^{2}=AC^{2}+BC^{2}$，
所以$AC^{2}=AB^{2}-BC^{2}=5^{2}-3^{2}=4^{2}$. 所以$AC = 4m$.
在$Rt\triangle A'B'C$中，$\angle C = 90^{\circ}$，$A'C = AC - AA' = 4 - 1 = 3(m)$，$A'B' = 5m$，
由勾股定理，得$A'B'^{2}=A'C^{2}+B'C^{2}$.
所以$B'C^{2}=A'B'^{2}-A'C^{2}=5^{2}-3^{2}=4^{2}$. 所以$B'C = 4m$.
所以$BB' = B'C - BC = 4 - 3 = 1(m)$.

3. 如图17-1-11所示，有一圆柱，高为8 cm，底面直径为4 cm，在圆柱下底面A点有一只蚂蚁，它想吃上底面与A相对的B点处的食物，需爬行的最短路程大约为(设π = 3)( )

A. 10 cm
B. 12 cm
C. 14 cm
D. 20 cm

答案：
A 解析：圆柱体的侧面展开图如图D - 17 - 2所示，
过B作$BG\perp AC$，则AB为爬行的最短路程，由题意，得$AB=\sqrt{8^{2}+6^{2}} = 10(cm)$.

4. 有一个长为12 cm，宽为4 cm，高为3 cm的长方体铁盒，在其内部放一根笔直的铁丝，则铁丝最长是________cm.

答案：
13 解析：如图D - 17 - 3所示，
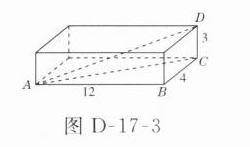
铁丝最长是A，D两点间的距离. 因为$AD^{2}=AC^{2}+DC^{2}$，$AC^{2}=AB^{2}+BC^{2}$，所以$AD^{2}=AB^{2}+BC^{2}+DC^{2}=12^{2}+4^{2}+3^{2}=13^{2}$，所以$AD = 13cm$.

5. 一艘帆船由于风向的原因先向正东方向航行了16 km，再向正北方向航行了12 km，这时它离出发点的距离为________km.

答案： 20 解析：由题意，得离出发点的距离为$\sqrt{16^{2}+12^{2}} = 20(km)$.

6. 在数轴上作出表示$\sqrt{26}$的点.

答案：
解：如图D - 17 - 4所示，
点A是表示$\sqrt{26}$的点.

1. 如果梯子的底端离建筑物的水平距离为9 m，那么长为15 m的梯子可以到达建筑物的高度是( )
A. 10 m
B. 11 m
C. 12 m
D. 13 m

答案： C 解析：由题意，得$\sqrt{15^{2}-9^{2}} = 12(m)$.

2. 如图17-1-12所示，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是( )

A. 2.5
B. 2$\sqrt{2}$
C. $\sqrt{3}$
D. $\sqrt{5}$

答案： D 解析：在$Rt\triangle OAB$中，由勾股定理，得$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$，所以这个交点表示的实数是$\sqrt{5}$.

3. 在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图17-1-13所示的直角梯形，其中三边长分别为2，4，3，则原直角三角形纸片的斜边长是( )

A. 10
B. 4$\sqrt{5}$
C. 10或4$\sqrt{5}$
D. 10或2$\sqrt{17}$

答案：
C 解析：原直角三角形纸片有如图D - 17 - 5①和图D - 17 - 5②所示的两种情况.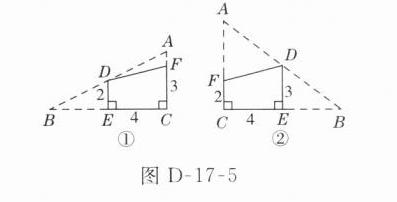
在图①中，D为AB的中点，$DE\perp BC$，$\angle C = 90^{\circ}$，所以E为BC的中点，$AC = 2DE = 4$，$BC = 2EC = 8$. 由勾股定理，得斜边$AB=\sqrt{4^{2}+8^{2}} = 4\sqrt{5}$.
在图②中，D为AB的中点，$DE\perp BC$于E，$\angle C = 90^{\circ}$，DE是$\triangle ABC$的中位线，所以$AC = 2DE = 6$，$BC = 2CE = 8$，所以$AB = 10$.