《2025年阳光课堂金牌练习册八年级数学下册人教版福建专版》

1. 如图18-1-2所示，在□ABCD中，E是AB延长线上一点，若∠D = 120°，则∠1等于( )


A. 120°
B. 60°
C. 45°
D. 30°

答案： B 解析：在$\square ABCD$中，$\because\angle D = 120^{\circ}$，$\therefore\angle ABC = 120^{\circ}$，$\therefore\angle 1 = 60^{\circ}$。

2. 如图18-1-3所示，在□ABCD中，AE平分∠DAB，∠B = 100°，则∠DEA=( )

A. 100° B. 80° C. 60° D. 40°

答案： D 解析：在$\square ABCD$中，$\because\angle B = 100^{\circ}$，$\therefore\angle DAB = 80^{\circ}$。$\because AE$平分$\angle DAB$，$\therefore\angle DAE=\angle EAB=\frac{1}{2}\angle DAB = 40^{\circ}$。$\because DC// AB$，$\therefore\angle DEA=\angle EAB = 40^{\circ}$。

3. 已知□ABCD的周长为32 cm，△ABC的周长为22 cm，则AC的长为( )
A. 11 cm
B. 4 cm
C. 6 cm
D. 5 cm

答案： C 解析：因为$\square ABCD$的周长为$32\ cm$，所以$AB + BC = 16\ cm$。又因为$\triangle ABC$的周长为$22\ cm$，即$AB + BC + AC = 22\ cm$，所以$AC = 6\ cm$。

4. 如图18-1-4所示，在□ABCD中，AD = 5，AB = 3，AE平分∠BAD交BC于点E，则线段BE，CE的长度分别为( )

A. 2，3
B. 3，2
C. 4，1
D. 1，4

答案： B 解析：因为$AE$平分$\angle BAD$，所以$\angle BAE=\angle DAE$。因为四边形$ABCD$是平行四边形，所以$AD// BC$，所以$\angle DAE=\angle AEB$，所以$\angle AEB=\angle BAE$，所以$AB = BE$。又因为$AB = 3$，所以$BE = 3$，$CE = BC - BE = 5 - 3 = 2$。

5. □ABCD的周长是44 cm，AB比AD长2 cm，那么AB = ______，AD = ______.

答案： $12\ cm$ $10\ cm$ 解析：$\because\square ABCD$的周长是$44\ cm$，$\therefore AB + AD = 22\ cm$。又$\because AB$比$AD$长$2\ cm$，即$AB - AD = 2\ cm$，$\therefore AB = 12\ cm$，$AD = 10\ cm$。

6. 如图18-1-5所示，∠A + ∠C = 80°，□ABCD的周长为40 cm，且AB - BC = 2 cm，求□ABCD的各边长和各内角的度数.

答案： 解：在$\square ABCD$中，$\because\angle A=\angle C$，$\angle A+\angle C = 80^{\circ}$，$\therefore\angle A=\angle C = 40^{\circ}$。又$\because\angle A+\angle D = 180^{\circ}$，$\therefore\angle D = 140^{\circ}$，$\therefore\angle B=\angle D = 140^{\circ}$。$\because\square ABCD$的周长为$40\ cm$，$\therefore AB + BC = 20\ cm$。又$\because AB - BC = 2\ cm$，$\therefore AB = 11\ cm$，$BC = 9\ cm$，$\therefore\square ABCD$的各边长为$AB = DC = 11\ cm$，$BC = AD = 9\ cm$。

1. 在□ABCD中，若∠A比∠B大16°，则∠C等于( )
A. 84°
B. 98°
C. 82°
D. 96°

答案： B 解析：设$\angle B = x^{\circ}$，则$\angle A = x^{\circ}+16^{\circ}$。在$\square ABCD$中，$\because\angle A+\angle B = 180^{\circ}$，$\therefore 2x^{\circ}+16^{\circ}=180^{\circ}$，$\therefore x^{\circ}=82^{\circ}$，$\therefore\angle A = 82^{\circ}+16^{\circ}=98^{\circ}$。$\because\angle C=\angle A$，$\therefore\angle C = 98^{\circ}$。

2. 在□ABCD中，∠A：∠B：∠C：∠D的值可以是( )
A. 1：2：3：4
B. 1：2：2：1
C. 2：2：1：1
D. 2：1：2：1

答案： D 解析：在$\square ABCD$中，$\angle A$与$\angle C$是对角，$\therefore\angle A=\angle C$。同理$\angle B=\angle D$。故选D。

3. 如图18-1-6所示，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD = 53°，则∠BCE等于( )



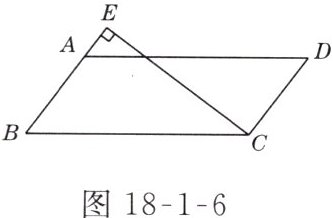
A. 53°
B. 37°
C. 47°
D. 123°

答案： B 解析：$\because AD// BC$，$\therefore\angle B=\angle EAD = 53^{\circ}$。$\because CE\perp AB$，$\therefore\angle E = 90^{\circ}$。在$\triangle EBC$中，$\angle BCE = 90^{\circ}-\angle B = 90^{\circ}-53^{\circ}=37^{\circ}$。

4. 如图18-1-7所示，四边形ABCD是平行四边形，点E在边BC上，如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是( )

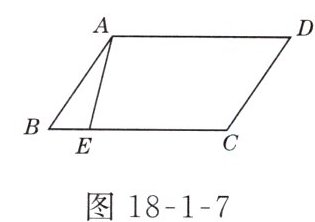
A. DF = BE B. AF = CE
C. CF = AE D. CF//AE

答案： C 解析：$\because$四边形$ABCD$是平行四边形，$\therefore AB = CD$，$\angle B=\angle D$。当$DF = BE$时，$\triangle CDF\cong\triangle ABE(SAS)$。故选项A中的条件能使$\triangle CDF$与$\triangle ABE$全等。当$AF = CE$时，得$DF = BE$，也能使$\triangle CDF\cong\triangle ABE$。若$CF// AE$，则$\angle BEA=\angle DFC$，也可证$\triangle CDF\cong\triangle ABE$。当$CF = AE$时，$\triangle CDF$与$\triangle ABE$不一定全等。

5. 已知□ABCD的周长为32，AB = 4，则BC=( )
A. 4
B. 12
C. 24
D. 28

答案： B 解析：根据平行四边形的性质，知$AB + BC=\frac{32}{2}=16$，所以$BC = 16 - AB = 16 - 4 = 12$。

6. 如图18-1-8所示，将□ABCD折叠，使顶点D恰好落在AB边上的点M处，折痕为AN，那么对于结论：①MN//BC，②MN = AM. 下列说法正确的是( )

A. ①②都对
B. ①②都错
C. ①对②错
D. ①错②对

答案： A 解析：由折叠可知，$\angle DAN=\angle NAM$，$\angle DNA=\angle ANM$。又$\because$四边形$ABCD$为平行四边形，$\therefore AB// CD$，$AD// BC$。$\therefore\angle DNA=\angle NAM$。$\therefore\angle DAN=\angle NAM=\angle DNA=\angle ANM$。$\therefore AD// MN$。$\therefore MN// BC$，即结论①正确。$\because\angle NAM=\angle ANM$，$\therefore MN = AM$，即结论②正确。故选A。