《2025年超能学典计算加解决问题六年级数学下册苏教版》

1. 口算。
　　7π = 　　　　　　　　1.26÷0.3 = 　　　　8.9×11 - 8.9 = 　　
　　π×$\frac{1}{5}$ = 　　　　　　87.5%×$\frac{1}{7}$ = 　　　　6×($\frac{1}{12}$ + 2) = 　　
　　47.1÷3.14 = 　　　　$\frac{7}{15}$÷$\frac{14}{25}$ = 　　　　　　$\frac{5}{7}$ + $\frac{5}{9}$×$\frac{9}{5}$ = 　　

答案： 21.98、4.2、89、0.628、0.125、12$\frac{1}{2}$、15、$\frac{5}{6}$、$\frac{81}{35}$

2. 递等式计算。(能简算的要简算)
　　$\frac{3}{4}$×[($\frac{7}{15}$ - $\frac{1}{5}$)÷$\frac{2}{3}$] 　　　　　　　　$\frac{16}{27}$×$\frac{1}{7}$ + $\frac{23}{27}$÷7×4

答案： 原式=$\frac{3}{4}$×($\frac{4}{15}$×$\frac{3}{2}$)-$\frac{3}{10}$ 原式=$\frac{4}{27}$×$\frac{4}{7}$+$\frac{23}{27}$×$\frac{4}{7}$=$\frac{4}{7}$×($\frac{4}{27}$+$\frac{23}{27}$)=$\frac{4}{7}$×1=$\frac{4}{7}$

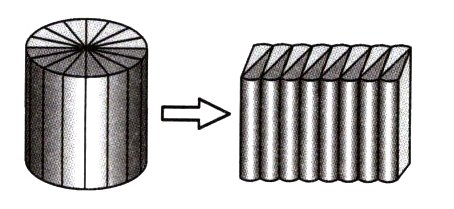
1. (基础题)把一个底面半径是6厘米的圆柱切拼成一个近似的长方体后(如图),表面积增加了180平方厘米。原来圆柱的体积是多少立方厘米?
　

答案： 180÷2÷6 = 15(厘米) π×6²×15 = 540π(立方厘米)(或1695.6立方厘米)

2. (重点题)一个长方体木块,长9厘米,宽6厘米,高8厘米。若把它加工成一个最大的圆锥,圆锥的体积是多少立方厘米?

答案： π×(8÷2)²×6×$\frac{1}{3}$ = 32π(立方厘米)(或100.48立方厘米)

3. (拓展题)一个底面直径10厘米、高20厘米的圆柱形容器内装有8厘米深的水,垂直放入一个长3厘米、宽3厘米、高15厘米的长方体铁块,使它触底(如图)。现在水深多少厘米？(保留整数)

答案： 3.14×(10÷2)²×8 = 628(立方厘米) 628÷[3.14×(10÷2)² - 3×3]≈9(厘米) 提示:铁块没有完全浸没在水中，但是水的体积不变，由于铁块的放入，水面上升，底面积 = 圆面积 - 正方形面积，水的体积÷底面积 = 水深。