《2025年超能学典计算加解决问题六年级数学下册苏教版》

1. 口算。
0.2π = 　　　　　　　1.5π = 　　　　　　　　π×0.5² = 　
785÷3.14 = 　　　　　2.512÷3.14 = 　　　　100.48÷3.14 = 　
24÷$\frac{3}{4}$ = 　　　　　　　$\frac{5}{16}$×$\frac{8}{15}$ = 　　　　　　$\frac{7}{4}$ + $\frac{1}{2}$ = 　

答案： 0.628　4.71　0.785　250　0.8　32　32　$\frac{1}{6}$　$\frac{9}{4}$

2. 递等式计算。
π×(37.68÷3.14÷2)²×5　　　　　2.3×1.5 + 4.5÷0.75

答案： 原式 = π×180 = 565.2
原式 = 3.45 + 6 = 9.45

1. (基础题)一个盛有水的圆柱形水桶的底面半径是20厘米，把一块铁块(完全浸没在水中)从水桶中取出后，水桶里水面下降了1厘米。这块铁块的体积是多少立方厘米?

答案： π×20²×1 = 400π(立方厘米)(或1256立方厘米)

2. (重点题)一个长方体木块，长25厘米，宽20厘米，高15厘米。
将这个木块加工成一个最大的圆柱，圆柱的体积是多少立方厘米?

答案： π×(20÷2)²×15 = 1500π(立方厘米)(或4710立方厘米)

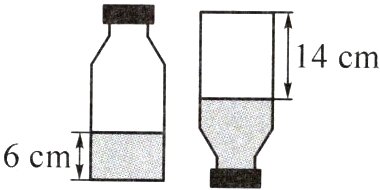
3. (拓展题)如图，为测量一个瓶子的容积，亮亮做了一个实验:量得瓶子底面的内直径为8厘米，瓶子正放时水面高6厘米，瓶子倒放时空着的部分高14厘米。这个瓶子的容积是多少立方厘米?

答案： π×(8÷2)²×(6 + 14) = 320π(立方厘米)(或1004.8立方厘米)
提示: 瓶子的容积等于水的体积 + 空着部分的体积，通过题中左图可得水的体积，通过题中右图可得空着部分的体积。