《2025年名校课堂九年级数学下册人教版安徽专版》

12.(8分)画出下列组合体的三视图.

答案：
解：如图所示.
　 　　　　　　
　

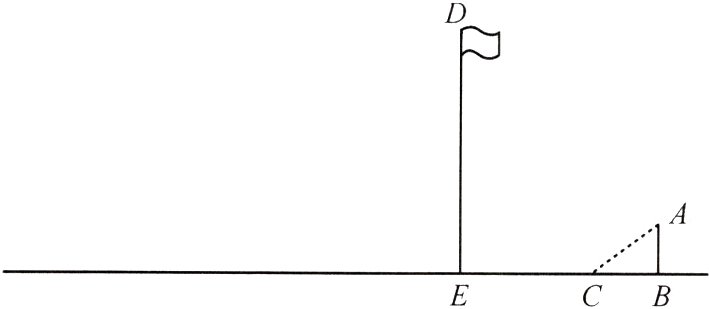
13.(12分) 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明落在地面上的影长为BC=2.4 m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG.
(2)若小明测得此刻旗杆落在地面的影长EG=16 m,请求出旗杆DE的高度.

答案： 解：
(1) 图略.
(2) $\because DG// AC$，$\therefore \angle G=\angle C$. $\therefore Rt\triangle ABC\sim Rt\triangle DEG$. $\therefore \frac{AB}{DE}=\frac{BC}{EG}$，即$\frac{1.6}{DE}=\frac{2.4}{16}$. 解得$DE = \frac{32}{3}$. 答：旗杆的高度为$\frac{32}{3}\ m$.

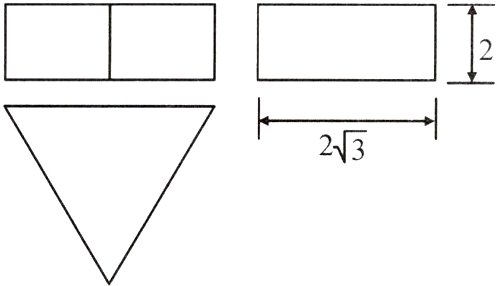
14.(14分)如图,这是某机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)如果俯视图中三角形为等边三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm²).

答案：
解：
(1) 直三棱柱.
(2) $\because \triangle ABC$是等边三角形，$CD\perp AB$，$CD = 2\sqrt{3}\ cm$，$\therefore AC=\frac{CD}{\sin60^{\circ}} = 4\ cm$. $\therefore S_{表}=4\times2\times3 + 2\times\frac{1}{2}\times4\times2\sqrt{3}=(24 + 8\sqrt{3})cm^{2}$.
　　　　　　　　　　　　　　　　　　　

15.(16分)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m,已知李明直立时的身高为1.75 m,求路灯的高CD的长.(结果精确到0.1 m)

答案： 解：设$CD = x\ m$. 由题意，得$AM\perp EC$，$CD\perp EC$，$BN\perp EC$，$EA = MA = 1.75$，$\therefore \angle E = 45^{\circ}$，$BN// CD$. $\therefore EC = CD = x$，$\triangle ABN\sim \triangle ACD$. $\therefore \frac{BN}{CD}=\frac{AB}{AC}$，即$\frac{1.75}{x}=\frac{1.25}{x - 1.75}$. 解得$x = 6.125\approx6.1$. 答：路灯的高$CD$的长约为$6.1\ m$.