《2025年名校课堂九年级数学下册人教版安徽专版》

1. 已知函数$y=(m - 2)x^{m^{2}-10}$是反比例函数，图象在第一、三象限内，则$m$的值是 （ ）
A. 3
B. -3
C. ±3
D. $-\frac{1}{3}$

答案： A

2. 若反比例函数$y=\frac{k}{x}$的图象经过点$A(4,1)$，则当$y＜1$时，$x$的取值范围是____________.

答案： $x＜0$ 或 $x＞4$

3. (2024·芜湖镜湖区模拟)如图，一次函数$y_{1}=kx + b(k\neq0)$与反比例函数$y_{2}=\frac{m}{x}(x＞0)$的图象交于$A(4,1)$，$B(\frac{1}{2},a)$两点.
(1)求这两个函数的解析式.
(2)根据图象，直接写出当$y_{1}-y_{2}＞0$时$x$的取值范围.
(3)点$P$在线段$AB$上，过点$P$作$x$轴的垂线，垂足为$M$，交反比例函数的图象于点$Q$. 若$\triangle POQ$的面积为 3，求点$P$的坐标.

答案： 解：
(1) $\because$ 反比例函数 $y_{2}=\frac{m}{x}(x ＞ 0)$ 的图象经过点 $A(4,1)$. $\therefore m = 4\times1 = 4$. $\therefore$ 反比例函数解析式为 $y_{2}=\frac{4}{x}(x ＞ 0)$. 把点 $B(\frac{1}{2},a)$ 代入 $y_{2}=\frac{4}{x}(x ＞ 0)$，得 $a = 8$，$\therefore$ 点 $B$ 的坐标为 $(\frac{1}{2},8)$. $\because$ 一次函数 $y_{1}=kx + b$ 的图象经过点 $A(4,1)$，$B(\frac{1}{2},8)$，$\therefore$
$\begin{cases}4k + b = 1\\\frac{1}{2}k + b = 8\end{cases}$ 解得 $\begin{cases}k = - 2\\b = 9\end{cases}$. $\therefore$ 一次函数的解析式为 $y_{1}=-2x + 9$.
(2) 由图象可得，$x$ 的取值范围是 $\frac{1}{2}＜x＜4$.
(3) 由题意，设 $P(p,-2p + 9)$ 且 $\frac{1}{2}\leq p\leq4$. $\therefore Q(p,\frac{4}{p})$. $\therefore PQ=-2p + 9-\frac{4}{p}$.
$\because S_{\triangle POQ}=3$，$\therefore\frac{1}{2}(-2p + 9-\frac{4}{p})\cdot p = 3$，解得 $p_{1}=\frac{5}{2}$，$p_{2}=2$.
$\therefore$ 点 $P$ 的坐标为 $(\frac{5}{2},4)$ 或 $(2,5)$.

4. 伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言：“给我一个支点，我可以撬动地球！”这句名言道出了“标杆原理”的意义和价值. “标杆原理”在实际生产和生活中，有着广泛的运用，比如：小明用撬棍撬动一块大石头，运用的就是“标杆原理”. 已知阻力$F_{1}(N)$和阻力臂$L_{1}(m)$的函数图象如图所示. 若小明想使动力$F_{2}$不超过 150 N，则动力臂$L_{2}$至少需要 （ ）

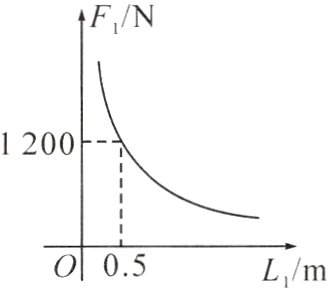
A. 2 m
B. 1 m
C. 6 m
D. 4 m

答案： D

5. 如图，四边形$OCDE$是边长为 2 的正方形，$\triangle EDF$是边长为 2 的等边三角形，点$G$，$H$分别是边$DE$，$DC$的中点，在$F$，$D$，$G$，$H$四个点中，位于同一反比例函数图象上的两个点是 （ ）

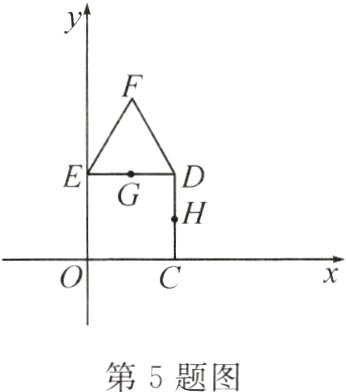
A. 点$F$和点$G$
B. 点$F$和点$D$
C. 点$F$和点$H$
D. 点$G$和点$H$

答案： D

6. 如图，$\square ABCD$的顶点$B$，$C$在坐标轴上，点$A$的坐标为$(-1,2\sqrt{3})$. 将$\square ABCD$沿$x$轴向右平移，得到$\square A'B'C'D'$，使点$A'$落在函数$y=\frac{4\sqrt{3}}{x}$的图象上. 若线段$BC$扫过的面积为 9，则点$B'$的坐标为________.

答案： $(3,3)$