《2025年名校课堂九年级数学下册人教版安徽专版》

1.(2024·池州开学)在Rt△ABC中，∠C = 90°，AC = 4，BC = 3，则tanA的值为 （ ）
A.$\frac{4}{3}$
B.$\frac{3}{4}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$

答案： B

2.(2023·亳州期末)如图，在△ABC中，∠ACB = 90°，CD⊥AB于点D，则下列结论正确的是 （ ）
A.sinA = $\frac{AB}{BC}$ B.sinB = $\frac{AD}{AC}$
C.cosA = $\frac{BD}{BC}$ D.cosB = $\frac{CD}{BD}$
　　 　　　

答案： B

3.如图，在网格图中，小正方形的边长均为1，点A，B，C都在格点上，则∠BAC的正切值是 （ ）


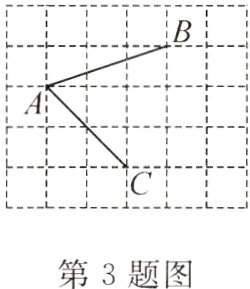
A.$\frac{1}{2}$
B.$\frac{\sqrt{5}}{2}$
C.$\frac{2\sqrt{5}}{5}$
D.2

答案： D

4.(2023·亳州利辛县期末)若∠A是锐角，sin(∠A + 15°) = $\frac{\sqrt{3}}{2}$，则tanA的值为 （ ）
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{3}$
C.1
D.$\frac{\sqrt{2}}{2}$

答案： C

5.若$\sqrt{\cos A - \frac{1}{2}} + |\sqrt{3}\tan B - 3| = 0$，则△ABC的形状是____________.

答案： 等边三角形

6.(2024·淮南月考)计算：$-1^{2024}$ + $\sqrt{2}$cos45° - $\sqrt{3}$tan30°.

答案： 解:原式=-1+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=-1+1-1=-1.

7.(2024·亳州一模)如图，在△ABC中，AB = 3$\sqrt{5}$，tan∠ABC = $\frac{1}{2}$，∠ACB = 45°，则BC的长为 （ ）

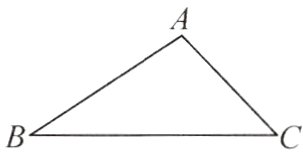
A.9
B.12
C.6$\sqrt{5}$
D.9$\sqrt{5}$　　　　

答案： A

8.如图，在△ABC中，∠A = 120°，AB = 4，AC = 2，则tanB的值是 （ ）

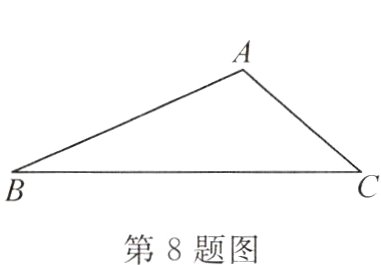
A.$\frac{\sqrt{21}}{14}$ B.$\frac{5\sqrt{7}}{14}$
C.$\frac{\sqrt{21}}{7}$ D.$\frac{\sqrt{3}}{5}$
　

答案： D

9.如图，在Rt△ABC中，∠C = 90°，BC = $\sqrt{5}$，点D是AC上一点，连接BD.若tan∠A = $\frac{1}{2}$，tan∠ABD = $\frac{1}{3}$，则CD的长为______.

答案： $\sqrt{5}$