《2025年名校课堂九年级数学下册人教版安徽专版》

【例】如图，△ABC是等腰三角形，AB过原点O，底边BC//x轴，双曲线y=$\frac{k}{x}$过A，B两点，过点C作CD//y轴交双曲线于点D. 若S_{△BCD}=12，则k的值是（ ）

A. -6
B. -12
C. -$\frac{9}{2}$
D. -9
【答案详解】第一步 设点：设点B的坐标为(b，$\frac{k}{b}$).
第二步 标其他点：过点A作AE⊥BC于点E，
∵AB过原点O，∴根据反比例函数图象的中心对称性，得A(__________).
∵△ABC是等腰三角形，
∴CE=BE=______.
∴BC = 4b，点D和点C的横坐标为________.
∴C(-3b，$\frac{k}{b}$).
∵底边BC//x轴，CD//y轴，
∴S_{△BCD}=$\frac{1}{2}$BC·CD=$\frac{1}{2}$×4b·CD=12.
∴CD=__________.
∴点D的纵坐标为__________.
∴D(__________).
第三步 列方程：∴k = __________·__________，
解得k=________.

答案： C
@@$-b,-\frac{k}{b}$　2b　-3b　$\frac{6}{b}$　$\frac{6 + k}{b}$　$-3b,\frac{6 + k}{b}$　-3b　$\frac{6 + k}{b}$　$-\frac{9}{2}$

1.（2023·绥化）在平面直角坐标系中，点A在y轴的正半轴上，AC//x轴，点B，C的横坐标都是3，BC=2，点D在AC上，且其横坐标为1.若反比例函数y=$\frac{k}{x}$(x＞0)的图象经过点B，D，则k的值是（ ）

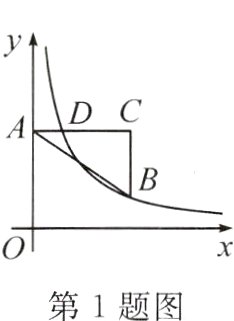
A. 1
B. 2
C. 3
D. $\frac{3}{2}$

答案： C

2. 如图，若反比例函数y=$\frac{\sqrt{3}}{x}$(x＞0)的图象经过等边三角形POQ的顶点P，则△POQ的边长为____.

答案： 2

3.（2023·池州贵池区模拟）如图，平行于y轴的直线与函数y_{1}=$\frac{k}{x}$(x＞0)和y_{2}=$\frac{2}{x}$(x＞0)的图象分别交于A，B两点，OA交双曲线y_{2}=$\frac{2}{x}$于点C，连接CD. 若△OCD的面积为2，则k=____.

答案： 8

4.（2022·安徽）如图，▱OABC的顶点O是坐标原点，A在x轴的正半轴上，B，C在第一象限，反比例函数y=$\frac{1}{x}$的图象经过点C，y=$\frac{k}{x}$(k≠0)的图象经过点B. 若OC=AC，则k=____.

答案： 3