《2025年名校课堂九年级数学下册人教版安徽专版》

1.【应用意识】【综合与实践】
主题：X型晒衣架稳固性检测.
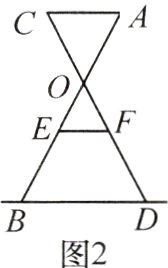
步骤：如图1所示的是晒衣架的实物图，图2是晒衣架的侧面示意图，立杆AB，CD相交于点O，经测量，得到AB=CD=136 cm，OA=OC=51 cm，OE=OF=34 cm. 现将晒衣架完全稳固张开，横扣链EF成一条线段，测得EF=32 cm.
证明与计算：
(1)连接AC，求证：AC//EF.
(2)利用夹子垂挂在晒衣架上的连衣裙（夹子高度忽略不计）总长度小于多少时，连衣裙才不会拖在地面上？
　

答案： 解：
(1)证明：
∵∠AOC = ∠EOF，$\frac{OA}{OE}=\frac{OC}{OF}=\frac{51}{34}=\frac{3}{2}$，
∴△AOC∽△EOF.
∴∠OAC = ∠OEF.
∴AC//EF.
(2)过点A作AM⊥BD于点M，过点O作ON⊥EF于点N.
∵OE = OF = 34 cm，
∴△OEF是等腰三角形.
∴∠OEF = $\frac{1}{2}(180^{\circ}-∠EOF)$.
∵ON⊥EF，EF = 32 cm，
∴ON是边EF上的中线.
∴EN = 16 cm. 在Rt△OEN中，根据勾股定理，得ON = $\sqrt{OE^{2}-EN^{2}}=\sqrt{34^{2}-16^{2}} = 30$ (cm).
∵ON⊥EF，AM⊥BD，
∴∠ONE = ∠AMB = 90°.
∵OA = OC，AB = CD，
∴OB = OD.
∴∠OBD = $\frac{1}{2}(180^{\circ}-∠BOD)$.
∴∠OBD = ∠OEF.
∴△EON∽△BAM.
∴$\frac{OE}{AB}=\frac{ON}{AM}$，即$\frac{34}{136}=\frac{30}{AM}$，解得AM = 120. 答：利用夹子垂挂在晒衣架上的连衣裙总长度小于120 cm时，连衣裙才不会拖在地面上.

2.【应用意识】如图所示的是幸福小区入口处安装的汽车出入道闸示意图. 如图1，道闸关闭时，四边形ABCD是矩形. 如图2，在道闸打开的过程中，边AD固定，AD⊥直线l，连杆AB，CD分别绕点A，D转动，且边BC始终与边AD平行，P为CD上的一点（不与点C，D重合），过点P作PE⊥直线l，PF⊥MN，垂足分别为E，F，即四边形PENF是矩形，过点D作DQ⊥PE，垂足为Q，延长BC与PF相交于点R.
(1)△PDQ与△CPR相似吗？请判断并说明理由.
(2)若道闸长AB=4米，宽AD=1米，点D距地面0.2米，PE=1.16米，RF=0.8米，CR=1.44米.
①点B到地面l的距离为______米；
②求PF的长.
　　　　　　　　　　 　

答案： 解：
(1)相似. 理由：
∵四边形PENF是矩形，
∴PF//l，PE//MN.
∵DQ⊥PQ，
∴DQ//PF.
∴∠CPR = ∠PDQ.
∵AD⊥l，BR//AD，PF//l，
∴BR⊥PF.
∴∠CRP = ∠PQD = 90°.
∴△PDQ∽△CPR.
(2)①3.6 ②
∵道闸长AB = 4米，
∴设PC = x米，则DP = (4 - x)米. 由
(1)知，△PDQ∽△CPR，
∴$\frac{PQ}{CR}=\frac{PD}{CP}$.
∵点D距地面0.2米，PE = 1.16米，CR = 1.44米，
∴PQ = PE - QE = 1.16 - 0.2 = 0.96(米).
∴$\frac{0.96}{1.44}=\frac{4 - x}{x}$，解得x = 2.4. 在Rt△CPR中，
∵CR = 1.44米，PC = 2.4米，
∴PR = $\sqrt{PC^{2}-CR^{2}}=\sqrt{2.4^{2}-1.44^{2}} = 1.92$ (米).
∴PF = PR + RF = 1.92 + 0.8 = 2.72(米).
∴PF的长为2.72米.