《2025年名校课堂九年级数学下册人教版安徽专版》

11.【空间观念】如图，在三角形纸片ABC中，∠A = 76°，∠B = 34°. 将三角形纸片沿某处剪开，下列四种剪法中，剪下的阴影三角形与原三角形相似的是（　　）
　
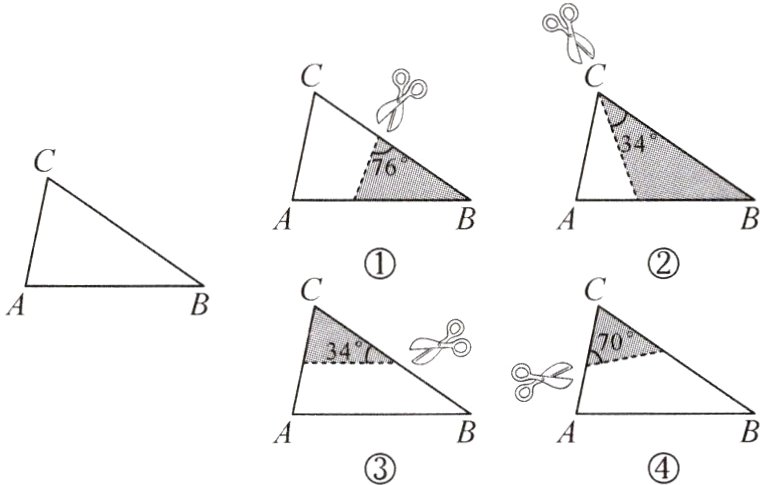
A. ①②　
B. ②④　
C. ①③　
D. ③④

答案： C

12.（教材P35例2变式）如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E. 若OE = 3，OB = 5，则CD的长为________.
　 　　　

答案： 9.6

13. 如图，在矩形ABCD中，AB = 6 cm，BC = 9 cm，点E，F分别在边AB，BC上，AE = 2 cm，BD，EF交于点G. 若G是EF的中点，则BG的长为______cm.

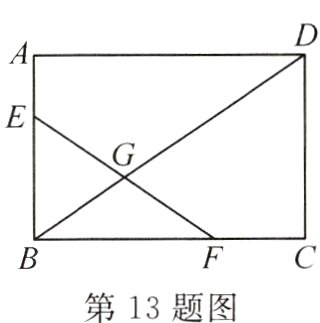
答案： $\sqrt{13}$

14.（2023·合肥包河区期末）如图，在△ABC中，D为BC上一点，E为AD上一点，如果∠DAC = ∠B，CD = CE.
　　(1)求证：△ACE∽△BAD.
　　(2)若CE = 3，BD = 4，AE = 2，求ED的长.
　　　　　　　　　　　　　

答案： 解：
(1)证明：
∵CD = CE，
∴∠CDE = ∠CED.
∵∠ADB = 180° - ∠CDE，∠AEC = 180° - ∠CED，
∴∠ADB = ∠AEC.
∵∠DAC = ∠B，
∴△ACE∽△BAD.
(2)
∵△ACE∽△BAD，
∴$\frac{AE}{CE}=\frac{BD}{AD}$.
∵CE = 3，BD = 4，AE = 2，
∴$AD=\frac{BD\cdot CE}{AE}=\frac{4×3}{2}=6$.
∴ED = AD - AE = 6 - 2 = 4.

15.【类比思想】如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC = ∠EDF = 90°，△DEF的顶点E与△ABC的斜边BC的中点重合. 将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.
　　(1)如图1，当点Q在线段AC上时，求证：△BPE∽△CEQ.
　　(2)如图2，当点Q在线段CA的延长线上时.
　　　①求证：△BPE∽△CEQ；
　　　②若BP = 2，CQ = 9，求BC的长.
　　　　 　

答案： 解：
(1)证明：
∵△ABC与△DEF都是等腰直角三角形，
∴∠B = ∠C = ∠DEF = 45°.
∴∠BEP + ∠CEQ = 180° - 45° = 135°，∠BEP + ∠BPE = 180° - 45° = 135°.
∴∠BPE = ∠CEQ. 又
∵∠B = ∠C，
∴△BPE∽△CEQ.
(2)①证明：
∵∠BEF = ∠C + ∠CQE，∠BEF = ∠BEP + ∠DEF，且∠C = ∠DEF = 45°，
∴∠CQE = ∠BEP. 又
∵∠B = ∠C，
∴△BPE∽△CEQ. ②
∵△BPE∽△CEQ，
∴$\frac{BE}{CQ}=\frac{BP}{CE}$.
∴BE·CE = BP·CQ.
∵BE = CE，
∴$BE^{2}=BP\cdot CQ$.
∵BP = 2，CQ = 9，
∴$BE^{2}=2×9 = 18$.
∴$BE = 3\sqrt{2}$.
∴BC = 2BE = $6\sqrt{2}$.