《2025年名校课堂九年级数学下册人教版安徽专版》

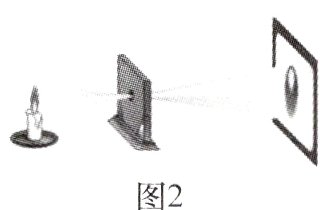
8. 【数学文化】(2024·合肥行知学校一模)大约在两千四五百年前，墨子和他的学生做了世界上第 1 个小孔成倒像的实验(如图 1)，解释了小孔成倒像的原理，并在《墨经》中有这样的记录：“景到，在午有端，与景长，说在端”.物理课上，小明记录了他和同桌所做的小孔成像实验数据(如图 2)：物距为 20 cm，像距为 30 cm，蜡烛火焰倒立的像的高度是 6 cm，则蜡烛火焰的高度是（ ）


A. 4 cm
B. 6 cm
C. 8 cm
D. 10 cm

答案： A

9. (2024·淮南月考)如图，在△ABC 中，∠ABC = 90°，∠A = 60°，直尺的一边与 BC 重合，另一边分别交 AB，AC 于点 D，E.点 B，C，D，E 处的读数分别为 15 cm，12 cm，0 cm，1 cm.则直尺宽 BD 的长为__________.

答案： $\frac{2}{3}\sqrt{3}$cm

10. 如图，小明在 A 时测得某树的影长为 8 m，B 时又测得该树的影长为 2 m.若两次日照的光线互相垂直，则树的高度为______.

答案： 4m

11. 【数学文化】(2023·阜阳临泉县期末)在《数书九章》中记载了一个测量塔高的问题：如图，AB 表示塔的高度，CD 表示竹竿顶端到地面的高度，EF 表示人到地面的高度，AB，CD，EF 在同一平面内，点 A，C，E 在一条水平直线上，已知 AC = 20 米，CE = 10 米，CD = 7 米，EF = 1.4 米，人从点 F 远眺塔顶 B，视线恰好经过竹竿的顶端 D.根据以上信息，求塔 AB 的高度.

答案： 解:过点F作FH⊥AB于点H，交CD于点G. 则FH⊥CD，AH = CG = EF = 1.4米，GH = AC = 20米，FG = CE = 10米，
∴∠DGF = ∠BHF = 90°.
∵CD = 7米，
∴DG = CD - CG = 7 - 1.4 = 5.6(米).
∵∠DFG = ∠BFH，
∴△FDG∽△FBH.
∴$\frac{DG}{BH}=\frac{FG}{FH}$.
∴$\frac{5.6}{BH}=\frac{10}{10 + 20}$.
∴BH = 16.8米.
∴AB = BH + AH = 16.8 + 1.4 = 18.2(米). 答:塔的高度为18.2米.

12. (教材 P58 复习题 T12 变式)阳光明媚的一天，实践课上，亮亮准备用所学知识测量教学楼前一座假山的高度 AB.如图，亮亮在地面上的点 F 处眼睛贴地观察，看到假山顶端 A、教学楼顶端 C 在一条直线上.此时他起身在点 F 处站直，发现自己的影子末端和教学楼的影子末端恰好重合于点 G 处，测得 FG = 2 米，亮亮的身高 EF 为 1.6 米.假山的底部 B 处因有花园围栏，无法到达，但经询问和进行部分测量后得知，BF = 9 米，点 D，B，F，G 在一条直线上，CD⊥DG，AB⊥DG，EF⊥DG.已知教学楼的高度 CD 为 16 米，请求出假山的高度 AB.

答案： 解:
∵CD⊥DG，EF⊥DG，
∴EF//CD.
∴△GEF∽△GCD.
∴$\frac{EF}{CD}=\frac{GF}{GD}$，即$\frac{1.6}{16}=\frac{2}{DB + 9 + 2}$，解得BD = 9.
∵CD⊥DG，AB⊥DG，
∴AB//CD.
∴△FAB∽△FCD.
∴$\frac{AB}{CD}=\frac{FB}{FD}$，即$\frac{AB}{16}=\frac{9}{9 + 9}$，解得AB = 8. 答:假山的高度AB为8米.