《2025年名校课堂九年级数学下册人教版安徽专版》

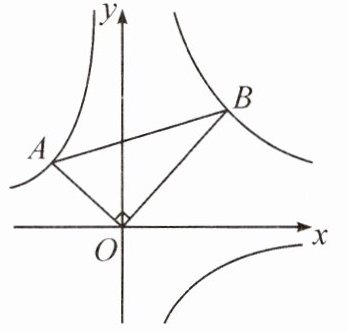
11.（2024·合肥50中三模）如图，把一块直角三角板（∠ABO = 30°）的直角顶点O放在坐标原点处，顶点A在函数$y_1=-\frac{1}{x}$的图象上，顶点B在函数$y_2=\frac{k}{x}$的图象上，则k = ______.

答案： 3

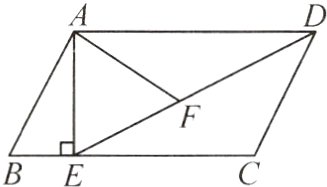
12. 如图，在▱ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE = ∠B.
（1）求证：△ADF∽△DEC.
（2）若$AB = 8，AD = 6\sqrt{3}，AF = 4\sqrt{3}$，求AE的长.

答案： 解:
(1)证明:
∵四边形ABCD是平行四边形，
∴AB//CD,AD//BC,
∴∠C + ∠B = 180°,∠ADF = ∠DEC.
∵∠AFD + ∠AFE = 180°,∠AFE = ∠B,
∴∠AFD = ∠C.
∴△ADF∽△DEC.
(2)
∵四边形ABCD是平行四边形，
∴CD = AB = 8.由
(1)知△ADF∽△DEC，
∴$\frac{AD}{DE}=\frac{AF}{CD}$，即$\frac{6\sqrt{3}}{DE}=\frac{4\sqrt{3}}{8}$.
∴DE = 12.
∵AD//BC，AE⊥BC，
∴AE⊥AD.
∴∠EAD = 90°.
∴AE = $\sqrt{DE^{2}-AD^{2}}=\sqrt{12^{2}-(6\sqrt{3})^{2}} = 6$.

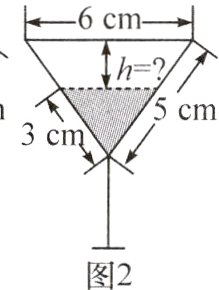
13.【模型观念】（2023·合肥庐阳区期末）如图，图1是装满了液体的高脚杯（数据如图），用去部分液体后，放在水平的桌面上如图2所示，此时液面距离杯口的距离h =（ ）

A. $\frac{8}{5}$ cm
B. 2 cm
C. $\frac{12}{5}$ cm
D. 3 cm

答案： A

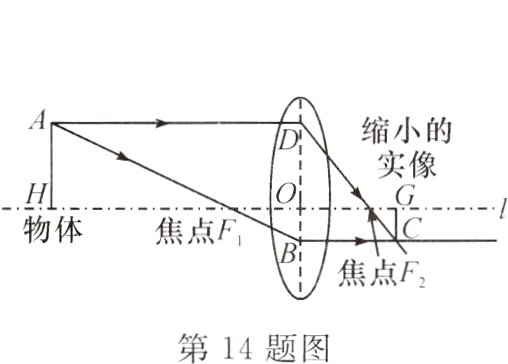
14.【跨学科·物理】凸透镜成像的原理如图所示，AD//l//BC. 若物体到焦点$F_1$的距离与焦点$F_1$到凸透镜中心线DB的距离之比为9:4（焦点$F_1$和$F_2$关于点O对称），则物体被缩小到原来的（ ）

A. $\frac{4}{5}$
B. $\frac{2}{5}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$

答案： C

15.（2024·浙江）如图，在平面直角坐标系中，△ABC与△A'B'C'是位似图形，位似中心为点O. 若点A（-3，1）的对应点为A'（-6，2），则点B（-2，4）的对应点B'的坐标为（ ）

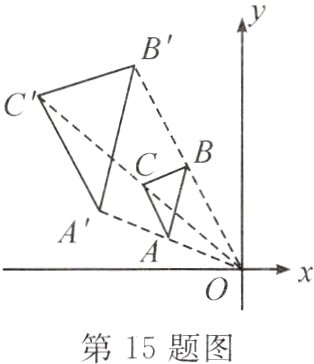
A.（-4，8）
B.（8，-4）
C.（-8，4）
D.（4，-8）

答案： A

16. 如图，以点O为位似中心，将五边形ABCDE放大后得到五边形A'B'C'D'E'. 已知OA = 10 cm，OA' = 20 cm，则五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是（ ）

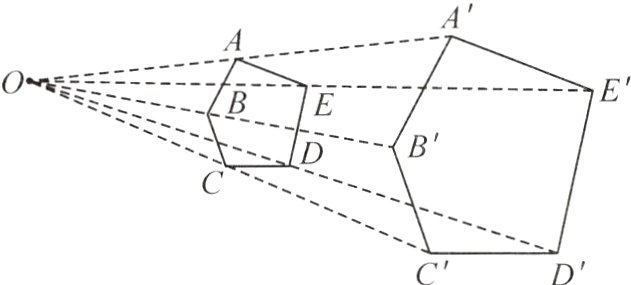
A. 1:2
B. 2:1
C. 1:3
D. 3:1

答案： A

17.【数学文化】《墨子·天文志》记载：“执规矩，以度天下之方圆. ”度方知圆，感悟数学之美. 如图，正方形ABCD的面积为4，以它的对角线的交点为位似中心，作它的位似图形A'B'C'D'. 若A'B':AB = 2:1，则四边形A'B'C'D'的外接圆的面积是________.

答案： 8π