《2025年名校课堂九年级数学下册人教版安徽专版》

9.（教材P65练习T2变式）把Rt△ABC三边的长度都扩大为原来的3倍，则锐角∠A的正弦值（ ）
A. 不变
B. 缩小为原来的$\frac{1}{3}$
C. 扩大为原来的3倍
D. 不能确定

答案： A

10. 在Rt△ABC中，∠C = 90°，sinA = $\frac{5}{13}$，则sinB的值为（ ）
A. $\frac{5}{13}$
B. $\frac{12}{13}$
C. $\frac{13}{5}$
D. $\frac{5}{12}$

答案： B

11. 如图，在Rt△ABC中，∠CAB = 90°，AD⊥BC于点D. 若BD = 2，sinC = $\frac{\sqrt{5}}{5}$，则线段AB的长为（ ）

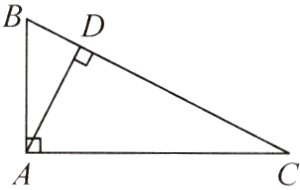
A. 10
B. 4
C. 4$\sqrt{5}$
D. 2$\sqrt{5}$　　

答案： D

12.（2023·芜湖无为市一模）如图，每个小正方形的边长为1，点A，B，C均在格点上，则sinB的值是（ ）
A. 1 B. $\frac{3}{4}$ C. $\frac{3}{5}$ D. $\frac{4}{5}$
　　

答案： C

13. 如图，在△ABC中，∠B为锐角，AB = 4$\sqrt{2}$，AC = 5，sinC = $\frac{4}{5}$，则BC的长为______.
　　　

答案： 7

14. 如图，菱形ABCD的周长为40 cm，DE⊥AB，sinC = $\frac{3}{5}$，求DE的长和菱形ABCD的面积.
　　　　　　　　　　　

答案： 解:$\because$菱形$ABCD$的周长为$40$cm，$\therefore AD = AB = 10$cm.$\because DE\perp AB$，$\therefore\angle AED = 90^{\circ}$.$\because$四边形$ABCD$为菱形，$\therefore\angle A=\angle C$.$\therefore$在$Rt\triangle AED$中，$\sin A=\sin C=\frac{DE}{AD}$，即$\frac{3}{5}=\frac{DE}{10}$. 解得$DE = 6$.$\therefore S_{菱形ABCD}=AB\cdot DE = 10\times6 = 60(cm^{2})$.

15. 如图，已知⊙O的半径为5 cm，弦AB的长为8 cm，P是AB延长线上的一点，BP = 2 cm，求sin∠OPA的值.
　　　　　　　　　　　　　

答案： 解:过点$O$作$OC\perp AB$于点$C$. 根据垂径定理，得$AC = BC=\frac{1}{2}AB = 4$cm.$\therefore CP = 4 + 2 = 6$(cm). 在$Rt\triangle OAC$中，根据勾股定理，得$OC=\sqrt{5^{2}-4^{2}} = 3$(cm). 在$Rt\triangle OCP$中，根据勾股定理，得$OP=\sqrt{OC^{2}+CP^{2}}=\sqrt{3^{2}+6^{2}} = 3\sqrt{5}$(cm).$\therefore\sin\angle OPA=\frac{OC}{OP}=\frac{3}{3\sqrt{5}}=\frac{\sqrt{5}}{5}$.

16. 如图，在矩形ABCD中，AB = 6，BC = 10，将矩形ABCD沿BE折叠，点A落在点A′处. 若EA′的延长线恰好过点C，则sin∠ABE的值为______.
　　　　　　　　　　　　　

答案： $\frac{\sqrt{10}}{10}$