《2025年名校课堂九年级数学下册人教版安徽专版》

8. 一圆锥的左视图如图所示，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为 （ ）

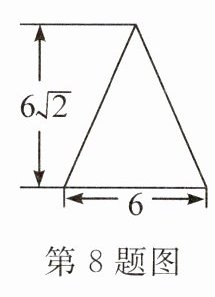
A. 90°　　　B. 120°　　C. 135°　　D. 150°

答案： B

9. 如图，这是一个长方体的三视图，则该长方体的体积是 （ ）

A. $m^{3}-3m^{2}+2m$ B. $m^{3}-2m$
C. $m^{3}+m^{2}-2m$ D. $m^{3}+m^{2}-m$

答案： C

10. 一个几何体的三视图如图所示，则该几何体的表面积是__________.
　

答案： $48\pi+64$

11. 如图所示的是由若干个棱长为1 cm的小正方体搭成的一个几何体三视图，则这个几何体的体积是____ $cm^{3}$.
　　　　　

答案： 6

12. 一个几何体的三视图如图所示，它的俯视图为菱形. 请写出该几何体的形状，并根据图中所给的数据求出它的侧面积.
　　　　　　　　　　　　　　

答案： 解:该几何体的形状是直四棱柱，由三视图知,棱柱底面菱形的对角线长分别为4 cm，3 cm，
∴菱形的边长为$\sqrt{(\frac{3}{2})^{2}+(\frac{4}{2})^{2}}=\frac{5}{2}(\text{cm})$.
∴$S_{侧}=\frac{5}{2}\times8\times4 = 80(\text{cm}^{2})$.

13. 一个几何体的三视图如图所示（单位：cm）.
　　　　　
　　(1)写出这个几何体的名称.
　　(2)根据图中所给数据计算这个几何体的表面积.
　　(3)如果一只蚂蚁要从这个几何体的点B出发，沿表面爬到AC的中点D，请你求出这个路线的最短路程.

答案：
解:
(1)圆锥
(2) $S_{表}=S_{扇形}+S_{圆}=\pi rl+\pi r^{2}=12\pi+4\pi = 16\pi(\text{cm}^{2})$.
(3)如图，将圆锥侧面展开，得到扇形$ABB'$，则线段$BD$的长即为所求的最短路程. 设$\angle BAB'=n^{\circ}$，连接$BC$. 由题意，得$\frac{n\pi\times6}{180}=4\pi$，解得$n = 120$.
∴$\angle BAB'=120^{\circ}$.
∵$C$为$\overset{\frown}{BB'}$的中点，
∴$\angle CAB = 60^{\circ}$. 又
∵$AC = AB$，
∴$\triangle ABC$是等边三角形.
∵$D$为$AC$的中点，
∴$\angle ADB = 90^{\circ}$，$BD = AB\cdot\sin60^{\circ}=3\sqrt{3}\text{ cm}$.
∴蚂蚁爬行路线的最短路程为$3\sqrt{3}\text{ cm}$.