《2025年名校课堂九年级数学下册人教版安徽专版》

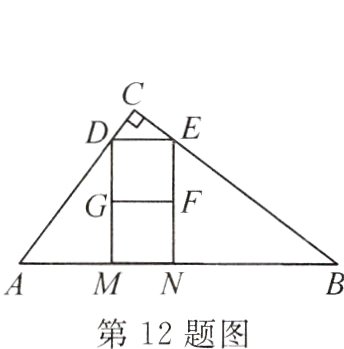
12.在Rt△ABC中，按如图所示方式放置两个正方形，使得顶点D，E，M，N均在三角形的边上.若AC=3，BC=4，则小正方形的边长为___________.

答案： $\frac{30}{31}$

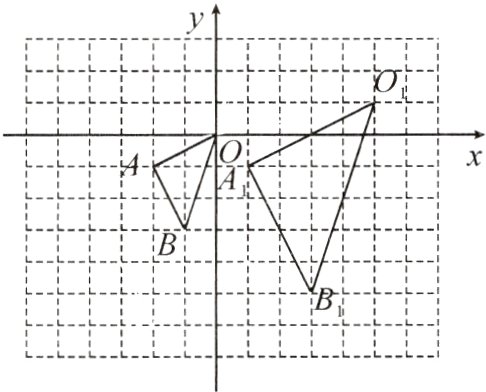
13.(10分)在如图所示的方格纸中，△OAB的顶点坐标分别为O(0，0)，A(－2，－1)，B(－1，－3)，△O₁A₁B₁与△OAB是以点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置，并写出点P及点B的对应点B₁的坐标.
(2)以原点O为位似中心，在y轴左侧画出△OAB的位似图形△OA₂B₂，使它与△OAB的相似比为2∶1，并写出点B的对应点B₂的坐标.

答案： 解：
(1)图略，P(-5,-1)，B₁(3,-5)。
(2)图略，B₂(-2,-6)。

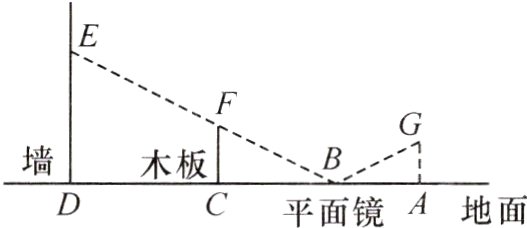
14.(14分)如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜，墙和木板均垂直于地面.手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处.点E到地面的高度DE=3.5 m，点F到地面的高度CF=1.5 m，灯泡到木板的水平距离AC=5.4 m，墙到木板的水平距离为CD=4 m.已知光在镜面反射中的入射角等于反射角，图中点A，B，C，D在同一直线上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.

答案： 解：
(1)由题意知，FC//DE，
∴△BFC∽△BED。
∴$\frac{BC}{BD}=\frac{FC}{ED}$，即$\frac{BC}{BC + 4}=\frac{1.5}{3.5}$。解得BC = 3。
∴BC的长为3 m。
(2)
∵AC = 5.4 m，
∴AB = 5.4 - 3 = 2.4(m)。
∵∠GBA = ∠FBC，∠GAB = ∠FCB = 90°，
∴△BGA∽△BFC。
∴$\frac{AG}{FC}=\frac{BA}{BC}$，即$\frac{AG}{1.5}=\frac{2.4}{3}$，解得AG = 1.2。答：灯泡到地面的高度AG为1.2 m。

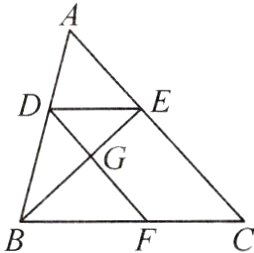
15.(16分)如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，DF，BE，DF与BE交于点G.已知四边形DFCE是平行四边形，且$\frac{DE}{BC}=\frac{2}{5}$.
(1)若AC=25，求线段AE，GF的长.
(2)若四边形GFCE的面积为48，求△ABC的面积.

答案： 解：
(1)
∵四边形DFCE是平行四边形，
∴DE//BC，DF//AC，DE = CF。
∴△ADE∽△ABC。
∴$\frac{AE}{AC}=\frac{DE}{BC}=\frac{2}{5}$。
∵AC = 25，
∴AE = 10。
∴CE = 25 - 10 = 15。
∵$\frac{DE}{BC}=\frac{CF}{BC}=\frac{2}{5}$，
∴$\frac{BF}{BC}=\frac{3}{5}$。
∵DF//AC，
∴△BFG∽△BCE。
∴$\frac{GF}{CE}=\frac{BF}{BC}=\frac{3}{5}$。
∴GF = 9。
(2)
∵△BFG∽△BCE，$\frac{BF}{BC}=\frac{3}{5}$，
∴$\frac{S_{\triangle BFG}}{S_{\triangle BCE}}=(\frac{3}{5})^2=\frac{9}{25}$。
∵$S_{\triangle BFG}+S_{四边形GFCE}=S_{\triangle BCE}$，
∴$\frac{S_{四边形GFCE}}{S_{\triangle BCE}}=\frac{16}{25}$。
∵四边形GFCE的面积为48，
∴$S_{\triangle BCE}=75$。
∵$\frac{AE}{AC}=\frac{2}{5}$，AE + CE = AC，
∴$\frac{CE}{AC}=\frac{3}{5}$。
∴$\frac{S_{\triangle BCE}}{S_{\triangle ABC}}=\frac{3}{5}$。
∴$S_{\triangle ABC}=125$。