《2025年金优教辅培优优选卷七年级数学上册人教版》

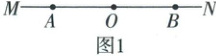
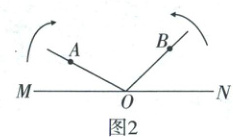
23. (11 分)如图 1, 点 $A$,$O$,$B$ 依次在直线 $MN$ 上, 现将射线 $OA$ 绕点 $O$ 沿顺时针方向以每秒 $4^{\circ}$ 的速度旋转, 同时射线 $OB$ 绕点 $O$ 沿逆时针方向以每秒 $6^{\circ}$ 的速度旋转, 直线 $MN$ 保持不动, 如图 2, 设旋转时间为 $t(0\leqslant t\leqslant 30$, 单位: 秒).
(1) 当 $t = 3$ 时, 求 $\angle AOB$ 的度数;
(2) 在运动过程中, 当 $\angle AOB$ 达到 $60^{\circ}$ 时, 求 $t$ 的值;
(3) 在旋转过程中是否存在这样的 $t$, 使得射线 $OB$ 与射线 $OA$ 组成的角为 $90^{\circ}$? 如果存在, 请直接写出 $t$ 的值; 如果不存在, 请说明理由.

答案： 23.解：
(1)当$t = 3$时，$\angle MOA = 4^{\circ} × 3 = 12^{\circ}$，$\angle NOB = 6^{\circ} × 3 = 18^{\circ}$，$\angle AOB = 180^{\circ} - \angle MOA - \angle NOB = 180^{\circ} - 12^{\circ} - 18^{\circ} = 150^{\circ}$. 所以$\angle AOB$的度数为$150^{\circ}$；
(2)当$\angle AOB = 60^{\circ}$时，①当第一次达到$60^{\circ}$时，$180^{\circ} - 4t - 6t = 60^{\circ}$，解得$t = 12$；②当第二次达到$60^{\circ}$时，$60^{\circ} + 180^{\circ} = 4t + 6t$，解得$t = 24$，综上，$t = 12s$或$24s$时，$\angle AOB$达到$60^{\circ}$；
(3)$t = 9$或27