《2025年金优教辅培优优选卷七年级数学上册人教版》

22. (10 分) 已知线段 $ AC $ 和 $ BC $ 在一条直线上, 如果 $ AC = 8cm $, $ BC = 3cm $, 求线段 $ AC $ 和 $ BC $ 的中点间的距离.

答案：
22.解:设AC、BC的中点分别为E、F,则由线段中点定义,得AE = EC = $\frac{1}{2}$AC,BF = FC = $\frac{1}{2}$BC.
(1)当点B在线段AC上时(如图①),则EF = EC - CF = $\frac{1}{2}$AC - $\frac{1}{2}$BC = $\frac{1}{2}$(AC - BC) = $\frac{1}{2}$×(8 - 3) = 2.5(cm);
(2)当点B在线段AC的延长线上时(如图②),则EF = EC + FC = $\frac{1}{2}$AC + $\frac{1}{2}$BC = $\frac{1}{2}$(AC + BC) = $\frac{1}{2}$×(8 + 3) = 5.5(cm).故线段AC和BC的中点间的距离为2.5cm或5.5cm.

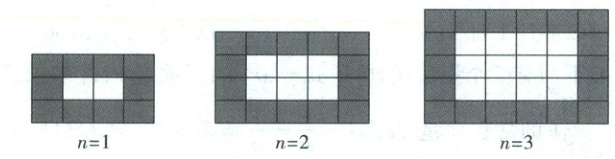
23. (10 分) 如图, 用同样规格黑白两色的正方形瓷砖铺设长方形地面, 请观察下列图形, 并探究和解答下列问题:
(1) 在第 $ n $ 个图形中, 每个横行共有 n + 3 块瓷砖, 每一竖列共有 n + 2 块瓷砖.
(2) 在铺设第 $ n $ 个图形中, 共有多少块瓷砖?
(3) 如果每块白瓷砖 3 元, 每块黑瓷砖 4 元, 则铺设 $ n = 10 $ 的图形时, 共需花多少元钱购买瓷砖.

答案： 23.解:
(1)n + 3 n + 2
(2)(n + 3)(n + 2)
(3)当n = 10时,总瓷砖数为13×12 = 156(块),其中白瓷砖数为10×11 = 110(块),黑瓷砖数为156 - 110 = 46(块),所需钱数为4×46 + 3×110 = 514(元).