2025年金优教辅培优优选卷七年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金优教辅培优优选卷七年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (9 分)如图,C,D 是线段 AB 上的两点,且满足$AC:CD:DB=3:2:1$,M,N 分别为 AC 和 CB 的中点.
(1)若$AB=24$,求 DN 的长度;
(2)证明:$5MN=6(CD+DN)$.
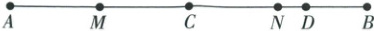
(1)若$AB=24$,求 DN 的长度;
(2)证明:$5MN=6(CD+DN)$.
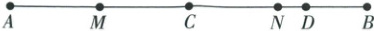
答案:
21.
(1)解:因为$AB = 24$,且$AC:CD:DB = 3:2:1$,所以$CD=\frac{2}{6}AB = 8$,$DB=\frac{1}{6}AB = 4$,所以$CB = CD + DB = 12$,因为点$N$为$CB$的中点,所以$CN=\frac{1}{2}CB = 6$,所以$ND = CD - CN = 8 - 6 = 2$.
(2)证明:因为$M$为$AC$的中点$N$为$CB$的中点,所以$MC=\frac{1}{2}AC$,$CN=\frac{1}{2}CB$,所以$MN = MC + CN=\frac{1}{2}AC+\frac{1}{2}CB=\frac{1}{2}AB$,因为$AC:CD:DB = 3:2:1$,所以$CD=\frac{2}{6}AB=\frac{1}{3}AB$,$DB=\frac{1}{6}AB$,所以$CB = CD + DB=\frac{1}{2}AB$,所以$CN=\frac{1}{2}CB=\frac{1}{2}×\frac{1}{2}AB=\frac{1}{4}AB$,所以$DN = CD - CN=\frac{1}{3}AB-\frac{1}{4}AB=\frac{1}{12}AB$,所以$6(CD + DN)=6×(\frac{1}{3}AB+\frac{1}{12}AB)=\frac{5}{2}AB$,又$5MN = 5×\frac{1}{2}AB=\frac{5}{2}AB$,所以$5MN = 6(CD + DN)$.
(1)解:因为$AB = 24$,且$AC:CD:DB = 3:2:1$,所以$CD=\frac{2}{6}AB = 8$,$DB=\frac{1}{6}AB = 4$,所以$CB = CD + DB = 12$,因为点$N$为$CB$的中点,所以$CN=\frac{1}{2}CB = 6$,所以$ND = CD - CN = 8 - 6 = 2$.
(2)证明:因为$M$为$AC$的中点$N$为$CB$的中点,所以$MC=\frac{1}{2}AC$,$CN=\frac{1}{2}CB$,所以$MN = MC + CN=\frac{1}{2}AC+\frac{1}{2}CB=\frac{1}{2}AB$,因为$AC:CD:DB = 3:2:1$,所以$CD=\frac{2}{6}AB=\frac{1}{3}AB$,$DB=\frac{1}{6}AB$,所以$CB = CD + DB=\frac{1}{2}AB$,所以$CN=\frac{1}{2}CB=\frac{1}{2}×\frac{1}{2}AB=\frac{1}{4}AB$,所以$DN = CD - CN=\frac{1}{3}AB-\frac{1}{4}AB=\frac{1}{12}AB$,所以$6(CD + DN)=6×(\frac{1}{3}AB+\frac{1}{12}AB)=\frac{5}{2}AB$,又$5MN = 5×\frac{1}{2}AB=\frac{5}{2}AB$,所以$5MN = 6(CD + DN)$.
22. (10 分)为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共 92 人(其中甲校的人数多于乙校的人数,且甲校的人数不足 90 人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表.

(1)如果两所学校分别单独购买服装一共应付 5000 元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有 10 名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.

(1)如果两所学校分别单独购买服装一共应付 5000 元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有 10 名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
答案:
22.解:
(1)设甲校$x$人,则乙校$(92 - x)$人,依题意得$50x + 60(92 - x)=5000$,解得$x = 52$,所以$92 - x = 40$,答:甲校有52人参加演出,乙校有40人参加演出.
(2)乙:$92 - 52 = 40$(人),甲:$52 - 10 = 42$(人),两校联合:$50×(40 + 42)=4100$(元),而此时比各自购买节约了:$(42×60 + 40×60)-4100 = 820$(元),若两校联合购买了91套只需:$40×91 = 3640$(元),此时又比联合购买每套节约:$4100 - 3640 = 460$(元).因此,最省钱的购买方案是两校联合购买91套服装,即比实际人数多买$91-(40 + 42)=9$(套).
(1)设甲校$x$人,则乙校$(92 - x)$人,依题意得$50x + 60(92 - x)=5000$,解得$x = 52$,所以$92 - x = 40$,答:甲校有52人参加演出,乙校有40人参加演出.
(2)乙:$92 - 52 = 40$(人),甲:$52 - 10 = 42$(人),两校联合:$50×(40 + 42)=4100$(元),而此时比各自购买节约了:$(42×60 + 40×60)-4100 = 820$(元),若两校联合购买了91套只需:$40×91 = 3640$(元),此时又比联合购买每套节约:$4100 - 3640 = 460$(元).因此,最省钱的购买方案是两校联合购买91套服装,即比实际人数多买$91-(40 + 42)=9$(套).
查看更多完整答案,请扫码查看


