第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
2. 如图,下列判断正确的是(
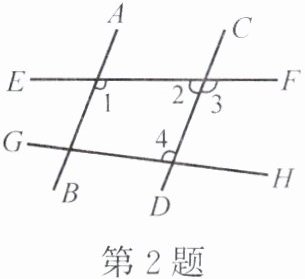
A.因为$\angle 1= \angle 2$,所以$AB// CD$
B.因为$\angle 1+\angle 2 = 180^{\circ}$,所以$AB// CD$
C.因为$\angle 3= \angle 4$,所以$AB// CD$
D.因为$\angle 1+\angle 4 = 180^{\circ}$,所以$AB// CD$
]
B
)。
A.因为$\angle 1= \angle 2$,所以$AB// CD$
B.因为$\angle 1+\angle 2 = 180^{\circ}$,所以$AB// CD$
C.因为$\angle 3= \angle 4$,所以$AB// CD$
D.因为$\angle 1+\angle 4 = 180^{\circ}$,所以$AB// CD$
]
答案:
B
3. 如图,给出下列条件:①$AC\perp AD$,$AC\perp BC$;②$\angle 1= \angle 2$,$\angle 3= \angle D$;③$\angle 4= \angle 5$;④$\angle BAD+\angle ABC = 180^{\circ}$。可以得到$AD// BC$的有(

A.①②③
B.②③④
C.①②④
D.①③④
]
C
)。
A.①②③
B.②③④
C.①②④
D.①③④
]
答案:
C
4. 同一平面内有直线$a_1$,$a_2$,$a_3$,$a_4$,…,$a_{100}$,$a_1\perp a_2$,$a_2// a_3$,$a_3\perp a_4$,$a_4// a_5$,…,按此规律推算,$a_1与a_{100}$的位置关系是(
A.平行
B.相交
C.重合
D.无法判断
A
)。A.平行
B.相交
C.重合
D.无法判断
答案:
A
5. 上完数学课后,小聪发现操场上旗杆的影子似乎与旁边一棵大树的影子平行,但他不能确定。此时最好的验证办法是(
A.找来三角尺、直尺,通过平移三角尺来验证影子是否平行
B.相信自己,两个影子就是平行的
C.构造几何模型,用学过的知识证明
D.作一直线去截两个影子,并用量角器量同位角的度数。若度数相等,则影子平行
D
)。A.找来三角尺、直尺,通过平移三角尺来验证影子是否平行
B.相信自己,两个影子就是平行的
C.构造几何模型,用学过的知识证明
D.作一直线去截两个影子,并用量角器量同位角的度数。若度数相等,则影子平行
答案:
D
6. 如图,$AD\perp BC于点D$,$EG\perp BC于点G$,$\angle 1= \angle E$。求证:$AD为\angle BAC$的平分线。(填空)

证明:因为$AD\perp BC$,$EG\perp BC$(已知),所以$\angle ADC= \angle EGC$。所以$AD// EG$(

证明:因为$AD\perp BC$,$EG\perp BC$(已知),所以$\angle ADC= \angle EGC$。所以$AD// EG$(
同位角相等,两直线平行
)。所以$\angle 1= \angle 2$(两直线平行,内错角相等
),$\angle 3= \angle E$(两直线平行,同位角相等
)。又因为$\angle 1= \angle E$(已知
),所以$\angle 2= $$\angle 3$
。所以$AD是\angle BAC$的平分线(角平分线的定义
)。
答案:
同位角相等,两直线平行 两直线平行,内错角相等 两直线平行,同位角相等 已知 ∠3 角平分线的定义
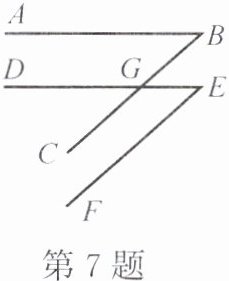
7. 如图,已知$AB// DE$,$\angle B= \angle E$。求证:$BC// EF$。
]
]

答案:
提示:证∠DGC(或∠BGE)=∠E
查看更多完整答案,请扫码查看


