《2025年预学与导学八年级数学上册浙教版》

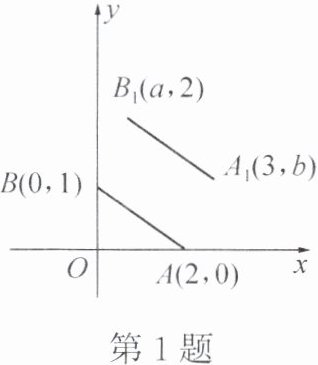
1. 如图,点$A$,$B的坐标分别为(2,0)$,$(0,1)$,如果将线段$AB平移至A_1B_1$,那么$a + b$的值为2。

答案： 2

2. $\triangle ABC的两个顶点A$,$B的坐标为A(1,1)$,$B(-1,2)$,将$\triangle ABC平移到\triangle A_1B_1C_1$。若$\triangle A_1B_1C_1的两个顶点B_1$,$C_1的坐标分别为B_1(1,-2)$,$C_1(m,n)$,则点$A_1$,$C$的坐标分别为$(3,-3)$,$(m-2,n+4)$。

答案： $(3,-3)$ $(m-2,n+4)$

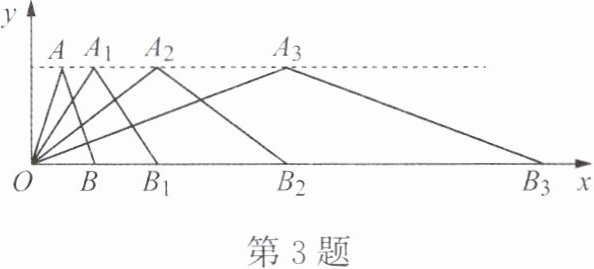
3. 如图,在平面直角坐标系中,第一次将$\triangle OAB变换成\triangle OA_1B_1$,第二次将$\triangle OA_1B_1变换成\triangle OA_2B_2$,第三次将$\triangle OA_2B_2变换成\triangle OA_3B_3$……已知$A(1,3)$,$A_1(2,3)$,$A_2(4,3)$,$A_3(8,3)$,$B(2,0)$,$B_1(4,0)$,$B_2(8,0)$,$B_3(16,0)$,按照此变换规律,第$n次变换后得到\triangle OA_nB_n$。其顶点$A_n$,$B_n的坐标为A_n$($2^{n}$,3),$B_n$($2^{n+1}$,0)。

答案： $2^{n}$ 3 $2^{n+1}$ 0

4. 把点$A(3,a - 1)向上平移5$个单位长度,所得的点与点$A向下平移1个单位长度所得的点关于x$轴对称,求$a$的值。

答案： $a=-1$

5. 已知点$P的坐标为(-4,3)$,先作点$P关于x轴对称的点P_1$,再将点$P_1向右平移8$个单位长度,得到点$P_2$,则点$P与点P_2之间的距离是10$。你认为这种说法对吗？请说明理由。

答案： 对。理由：$PP_{2}=\sqrt{PP_{1}^{2}+P_{1}P_{2}^{2}}=\sqrt{6^{2}+8^{2}}=10$