《2025年预学与导学八年级数学上册浙教版》

1. 已知等边三角形 $ ABC $ 的角平分线 $ AD = 12 $,$ P $ 是 $ \triangle ABC $ 内任意一点,则点 $ P $ 到 $ \triangle ABC $ 的三边的距离之和为12。

答案： 12

2. 如图,已知 $ AB = AC $,$ BD = DC $,$ AE $ 平分 $ \angle FAB $。$ AE $ 与 $ AD $ 是否垂直？为什么？

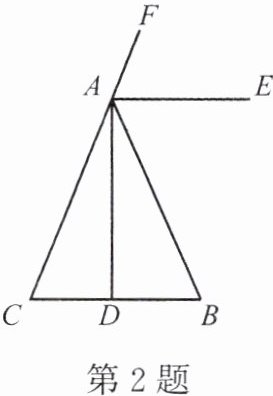
答案： 垂直，理由略

3. 如图,在等腰三角形 $ ABC $ 中,$ CH $ 是底边 $ AB $ 上的高线,$ P $ 是线段 $ CH $ 上不与端点重合的任意一点,连结 $ AP $ 并延长,交 $ BC $ 于点 $ E $,连结 $ BP $ 并延长,交 $ AC $ 于点 $ F $。求证：
(1) $ \angle CAE = \angle CBF $。
(2) $ PE = PF $。

答案： 1. 证明$\angle CAE=\angle CBF$：
解（证明）：
因为$\triangle ABC$是等腰三角形，$CH$是底边$AB$上的高线，根据等腰三角形三线合一的性质，所以$AC = BC$，$\angle ACP=\angle BCP$。
在$\triangle ACP$和$\triangle BCP$中，$\begin{cases}AC = BC\\\angle ACP=\angle BCP\\CP = CP\end{cases}$（公共边）。
根据$SAS$（边角边）定理，可得$\triangle ACP\cong\triangle BCP$。
由全等三角形的对应角相等，所以$\angle CAP=\angle CBP$，即$\angle CAE=\angle CBF$。
2. 证明$PE = PF$：
解（证明）：
在$\triangle ACE$和$\triangle BCF$中，$\begin{cases}\angle ACE=\angle BCF\\AC = BC\\\angle CAE=\angle CBF\end{cases}$（已证$\angle CAE=\angle CBF$，等腰三角形$AC = BC$，公共角$\angle ACE=\angle BCF$）。
根据$ASA$（角边角）定理，可得$\triangle ACE\cong\triangle BCF$。
所以$AE = BF$（全等三角形对应边相等）。
又因为$\triangle ACP\cong\triangle BCP$，所以$AP = BP$。
那么$AE - AP=BF - BP$。
即$PE = PF$。
综上，（1）$\angle CAE=\angle CBF$得证；（2）$PE = PF$得证。

4. 如图,$ AB = AC $,$ \angle BAC = 90^{\circ} $,$ \angle 1 = \angle 2 $,$ CE \perp BE $,$ AC $ 与 $ BE $ 相交于点 $ D $。求证：$ BD = 2CE $。

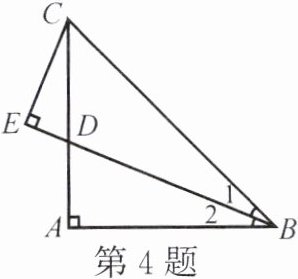
答案： 提示:延长CE,BA交于点F。证△BEC≌△BFE,得CE=EF=$\frac{1}{2}$CF,再证△BAD≌△CAF,得BD=CF=2CE