《2025年预学与导学八年级数学上册浙教版》

1. 如图,在等腰三角形 $ABC$ 中,$AB = AC$,$AD$ 是底边 $BC$ 上的高线。已知 $AB = 5$ cm,$BC = 6$ cm,则 $AD= $4cm。

答案： 4

2. 小慧在操场上向东走 80 米后,又向北或南(填方向)直走 60 米,再往原地方向直走 100 米就回到原地。

答案： 北或南

3. 在 $\triangle ABC$ 中,$\angle A$,$\angle B$,$\angle C$ 的对边分别为 $a$,$b$,$c$。给出下列条件：① $\angle A-\angle B= \angle C$,② $a^{2}-b^{2}= c^{2}$,③ $\angle A:\angle B:\angle C = 3:4:5$,④ $a:b:c = 3:4:5$,⑤ $\angle A = 2\angle B$,$c = 2b$。其中能使 $\triangle ABC$ 成为直角三角形的是①②④⑤。(填序号)

答案： ①②④⑤

4. 如果一个三角形中的一个角的度数是另一个角的 3 倍,那么我们称这个三角形为“智慧三角形”。下列各组数据中,能作为智慧三角形三边长的一组是(D)。
A.$1$,$2$,$3$
B.$1$,$1$,$\sqrt{2}$
C.$1$,$1$,$\sqrt{3}$
D.$1$,$2$,$\sqrt{3}$

答案： D

5. 判定以下列 $a$,$b$,$c$ 为边的三角形是否为直角三角形。
(1)$a = 6$,$b = 8$,$c = 10$。
(2)$a = 6$,$b = 8$,$c= \sqrt{28}$。

答案：
(1)是。提示:$a^{2}+b^{2}=c^{2}$
(2)是。提示:$a^{2}+c^{2}=b^{2}$

6. 如图,在 $\triangle ABC$ 中,$CD\perp AB$ 于点 $D$,$AC = 20$,$BC = 15$,$BD = 9$。求证：$\triangle ABC$ 是直角三角形。

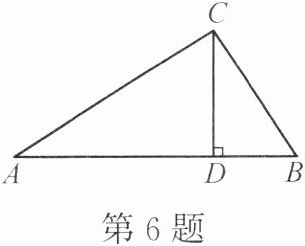
答案： 提示:先求CD=12,再求AD=16,由$AB^{2}=AC^{2}+BC^{2}$得证

7. 如图,在正方形 $ABCD$ 中,$F$ 为 $DC$ 的中点,$E$ 为 $CB$ 的四等分点,即 $CE= \frac{1}{4}CB$。求证：$\triangle AEF$ 是直角三角形。

答案： 提示:连结AE，由勾股定理逆定理可证明△AEF为直角三角形