《2025年预学与导学八年级数学上册浙教版》

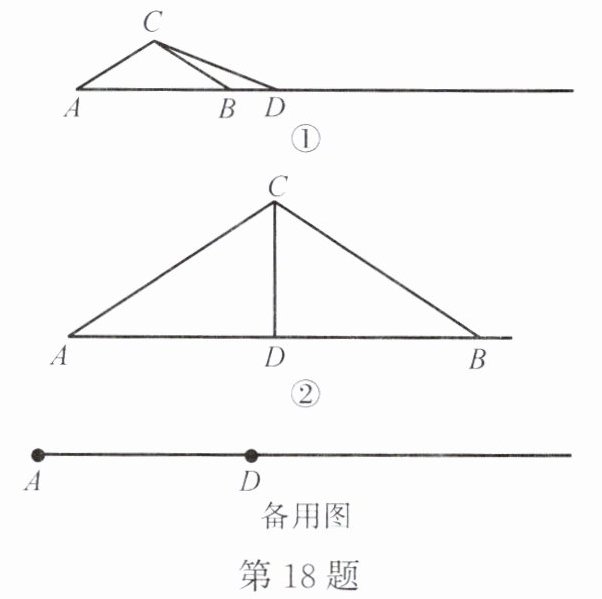
18. 如图①,已知线段$AD = 5$,点$B从点A$处出发,沿射线$AD$方向运动,以$AB为底作等腰三角形ABC$,使得$AC = BC = \frac{3}{5}AB$。
(1) 如图②,当$AB = 10$时,求证：$CD\perp AB$。
(2) 当$\triangle BCD是以BC$为腰的等腰三角形时,求$BC$的长。
(3) 当$AB＞5$时,在线段$BC上是否存在点E$,使得$\triangle BDE与\triangle ACD$全等？若存在,求出$BC$的长；若不存在,请说明理由。
(4) 作点$A关于直线CD的对称点A'$,连结$CA'$,当$CA'// AB$时,求$CA'$的长。

答案： 1. （1）证明：
已知$AB = 10$，$AC = BC=\frac{3}{5}AB$，则$AC = BC = 6$。
因为$AD = 5$，所以$BD=AB - AD=10 - 5 = 5$。
在$\triangle ACD$和$\triangle BCD$中，$\left\{\begin{array}{l}AC = BC\\CD = CD\\AD = BD\end{array}\right.$。
根据$SSS$（边 - 边 - 边）全等判定定理，$\triangle ACD\cong\triangle BCD$。
所以$\angle ADC=\angle BDC$，又因为$\angle ADC+\angle BDC = 180^{\circ}$，所以$\angle ADC=\angle BDC = 90^{\circ}$，即$CD\perp AB$。
2. （2）设$AB=x$，则$AC = BC=\frac{3}{5}x$，$BD=\vert x - 5\vert$。
①当$BC = BD$时：
则$\frac{3}{5}x=\vert x - 5\vert$。
当$x-5\geq0$，即$x\geq5$时，$\frac{3}{5}x=x - 5$，移项得$x-\frac{3}{5}x = 5$，$\frac{2}{5}x = 5$，解得$x=\frac{25}{2}$，此时$BC=\frac{3}{5}×\frac{25}{2}=\frac{15}{2}$。
当$x - 5\lt0$，即$x\lt5$时，$\frac{3}{5}x=5 - x$，移项得$\frac{3}{5}x+x = 5$，$\frac{3x + 5x}{5}=5$，$\frac{8x}{5}=5$，$x=\frac{25}{8}$，此时$BC=\frac{3}{5}×\frac{25}{8}=\frac{15}{8}$。
②当$BC = CD$时：
过$C$作$CE\perp AB$于$E$，$AE = BE=\frac{1}{2}AB$（等腰三角形三线合一），设$AB=x$，则$AC = BC=\frac{3}{5}x$，$AE=\frac{x}{2}$，$AD = 5$，$DE=\vert\frac{x}{2}-5\vert$。
在$Rt\triangle ACE$中，$CE=\sqrt{AC^{2}-AE^{2}}=\sqrt{(\frac{3}{5}x)^{2}-(\frac{x}{2})^{2}}=\sqrt{\frac{9x^{2}}{25}-\frac{x^{2}}{4}}=\sqrt{\frac{36x^{2}-25x^{2}}{100}}=\sqrt{\frac{11x^{2}}{100}}=\frac{\sqrt{11}}{10}x$。
若$BC = CD$，在$Rt\triangle CED$中，$CD = BC=\frac{3}{5}x$，$CE=\frac{\sqrt{11}}{10}x$，$DE=\vert\frac{x}{2}-5\vert$，根据$CD^{2}=CE^{2}+DE^{2}$，$(\frac{3}{5}x)^{2}=(\frac{\sqrt{11}}{10}x)^{2}+(\frac{x}{2}-5)^{2}$。
$\frac{9x^{2}}{25}=\frac{11x^{2}}{100}+\frac{x^{2}}{4}-5x + 25$，通分$\frac{36x^{2}}{100}-\frac{11x^{2}}{100}-\frac{25x^{2}}{100}+5x - 25 = 0$，$5x-25 = 0$，解得$x = 5$（此时$BC = 3$，$CD=\sqrt{3^{2}-0^{2}} = 3$，$BD = 0$，$B$与$D$重合，舍去）。
综上，$BC$的长为$\frac{15}{2}$或$\frac{15}{8}$。
3. （3）假设$\triangle BDE\cong\triangle ACD$：
因为$\triangle BDE\cong\triangle ACD$，所以$BD = AC$，$BE = AD$。
设$AB=x$，则$AC = BC=\frac{3}{5}x$，$BD=x - 5$。
由$BD = AC$得$x - 5=\frac{3}{5}x$，移项得$x-\frac{3}{5}x = 5$，$\frac{2}{5}x = 5$，解得$x=\frac{25}{2}$，则$BC=\frac{3}{5}×\frac{25}{2}=\frac{15}{2}$。
此时$BE = AD = 5$，$BC=\frac{15}{2}$，$CE=BC - BE=\frac{15}{2}-5=\frac{5}{2}$。
在$Rt\triangle CED$（由（1）中方法可证$CD\perp AB$），$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{(\frac{15}{2})^{2}-5^{2}}=\sqrt{\frac{225 - 100}{4}}=\frac{5\sqrt{5}}{2}$，$DE=\sqrt{BD^{2}-BE^{2}}=\sqrt{(\frac{15}{2})^{2}-5^{2}}=\frac{5\sqrt{5}}{2}$（$BD=\frac{15}{2}$）。
所以存在点$E$，$BC$的长为$\frac{15}{2}$。
4. （4）因为点$A$与$A'$关于$CD$对称，所以$AC = A'C$，$AD = A'D = 5$，$\angle ACD=\angle A'CD$。
又因为$CA'// AB$，所以$\angle A'CD=\angle ADC$（内错角相等）。
由（1）知，当$CD\perp AB$时（设此时$AB=x$，$AC = BC=\frac{3}{5}x$，$AD = 5$，$BD=x - 5$，$\triangle ACD\cong\triangle BCD$），$\angle ACD=\angle BCD$，$\angle ADC = 90^{\circ}$，$\angle ACD=\angle A'CD = 45^{\circ}$，所以$\triangle ACD$是等腰直角三角形，则$AC = AD = 5$。
因为$AC = A'C$，所以$CA'=5$。
综上，（1）证明见上述过程；（2）$BC$的长为$\frac{15}{2}$或$\frac{15}{8}$；（3）存在，$BC=\frac{15}{2}$；（4）$CA' = 5$。