《2025年预学与导学八年级数学上册浙教版》

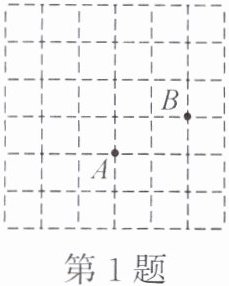
1. 如图,$A$,$B$ 是 $6×6$ 网格图中的两个格点(小正方形的顶点),图中每个小正方形的边长为 1。
(1)找一个格点 $D$,使 $\triangle ABD$ 为直角三角形,这样的点 $D$ 有7个。
(2)找一个格点 $E$,使 $\triangle ABE$ 的面积为 2,这样的点 $E$ 有5个。

答案：
(1)7
(2)5

2. 有下列三组数：① $1$,$\sqrt{2}$,$\sqrt{3}$；② $40$,$10x-\frac{1}{x}$,$10x+\frac{1}{x}$($x＞0$)；③ $n^{2}-1$,$2n$,$n^{2}+1$($n＞1$)。其中一定能作为直角三角形三边长的是①③。(填序号)

答案： ①③

3. 如图,$M$ 是等边三角形 $ABC$ 内一点,$E$ 是等边三角形 $ABC$ 外一点,连结 $MA$,$MB$,$MC$,$EB$,$EC$,已知 $MB = EB$,$\angle MBE = 60^{\circ}$。
(1)求证：$AM = CE$。
(2)若 $MA = 3$,$MB = 4$,$MC = 5$,求 $\angle AMB$ 的度数。

答案： 1. （1）证明：
因为$\angle MBE = 60^{\circ}$，$MB = EB$，所以$\triangle MBE$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形）。
则$\angle MBE=\angle ABC = 60^{\circ}$，$BM = BE$。
又因为$\angle ABC=\angle ABM+\angle MBC$，$\angle MBE=\angle CBE+\angle MBC$，所以$\angle ABM=\angle CBE$。
已知$\triangle ABC$是等边三角形，所以$AB = BC$。
在$\triangle ABM$和$\triangle CBE$中：
$\begin{cases}AB = BC\\\angle ABM=\angle CBE\\BM = BE\end{cases}$
根据$SAS$（边角边）定理，可得$\triangle ABM\cong\triangle CBE$。
所以$AM = CE$（全等三角形的对应边相等）。
2. （2）
由（1）知$\triangle MBE$是等边三角形，所以$ME = MB = 4$，$\angle BME = 60^{\circ}$。
又因为$AM = CE = 3$，$MC = 5$。
在$\triangle MCE$中，$ME^{2}+CE^{2}=4^{2}+3^{2}=16 + 9=25$，$MC^{2}=5^{2}=25$。
所以$ME^{2}+CE^{2}=MC^{2}$。
根据勾股定理的逆定理（若$a^{2}+b^{2}=c^{2}$，则以$a$，$b$，$c$为边的三角形是直角三角形，其中$c$为斜边），可得$\triangle MCE$是直角三角形，$\angle MEC = 90^{\circ}$。
因为$\triangle ABM\cong\triangle CBE$，所以$\angle AMB=\angle BEC$。
$\angle BEC=\angle BME+\angle MEC$。
所以$\angle AMB=60^{\circ}+90^{\circ}=150^{\circ}$。
综上，（1）已证$AM = CE$；（2）$\angle AMB$的度数为$150^{\circ}$。

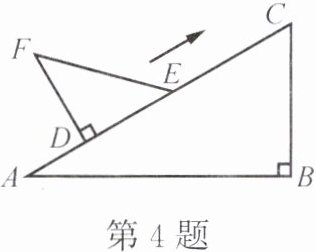
4. 如图,$\angle B = 90^{\circ}$,$\angle A = 30^{\circ}$,$BC = 6$ cm,$\angle EDF = 90^{\circ}$,$\angle FED = 45^{\circ}$,$DE = 4$ cm。将 $\triangle DEF$ 的直角边 $DE$ 与 $\triangle ABC$ 的斜边 $AC$ 重合,并将 $\triangle DEF$ 沿 $AC$ 方向移动。在 $\triangle DEF$ 移动的过程中,点 $D$,$E$ 始终在边 $AC$ 上(移动开始时点 $D$ 与点 $A$ 重合)。
(1)当 $\triangle DEF$ 移到什么位置,即 $AD$ 的长为多少时,点 $F$,$C$ 的连线与 $AB$ 平行？
(2)当 $\triangle DEF$ 移到什么位置,即 $AD$ 的长为多少时,以线段 $AD$,$FC$,$BC$ 的长为三边长的三角形是直角三角形？

小贴士：第(2)题中,$AD$,$FC$,$BC$ 三条线段中,哪条线段是斜边？

答案：
(1)$(12 - 4\sqrt{3})cm$
(2)设AD=x，当FC为斜边时,$x = \frac{31}{6}cm$;当AD为斜边时，$x = \frac{49}{6}＞8$，不符合题意;当BC为斜边时，$x^{2} - 12x + 62 = 0$，$(x - 6)^{2} = - 26＜0$，不符合题意