《2025年预学与导学八年级数学上册浙教版》

1. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ BC $ 的中点,$ DE \perp AB $ 于点 $ E $,$ DF \perp AC $ 于点 $ F $,则图中全等的三角形共有(B)。

A.2 对
B.3 对
C.4 对
D.5 对

答案： B

2. 下列说法中,正确的是(D)。
A.等腰三角形的高线、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形中一条边的长不可能是另一条边长的两倍
D.等腰三角形两个底角的平分线相等

答案： D

3. 在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ BC $ 的中点,$ \angle BAC = 100^{\circ} $,则 $ \angle BAD = $50°,$ \angle B = $40°,$ \angle ADB = $90°。

答案： 50°　40°　90°

4. 已知 $ \triangle ABC $ 的周长为 $ 36 \mathrm{cm} $,$ AB = AC $,$ AD \perp BC $,$ D $ 为垂足,$ \triangle ABD $ 的周长为 $ 30 \mathrm{cm} $,那么 $ AD $ 的长为12cm。

答案： 12cm

5. 如图,某大桥为三塔斜拉桥,中塔左右两边所挂的最长钢索 $ AB = AC $,塔柱与桥面交点 $ D $ 与点 $ B $ 之间的距离是 $ 228 \mathrm{m} $,则 $ BC $ 的长是456 $ \mathrm{m} $。

答案： 456

6. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD \perp BC $ 于点 $ D $,$ E $ 为 $ AD $ 上的任意一点,连结 $ BE $,$ CE $。求证：$ BE = CE $。(填空)
证明：在 $ \triangle ABC $ 中,
因为 $ AB = AC $,$ AD \perp BC $,
所以BD=DC(等腰三角形三线合一),
即 $ AD $ 垂直平分 $ BC $。
所以 $ BE = CE $(线段垂直平分线上的点到线段两端的距离相等)。

答案： BD=DC　等腰三角形三线合一　线段垂直平分线上的点到线段两端的距离相等

7. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ \triangle ABC $ 外一点,且 $ BD = CD $。求证：$ AD $ 垂直平分 $ BC $。

答案： 提示:证∠BAD=∠CAD,可由等腰三角形三线合一的性质证得

8. 如图,已知线段 $ a $ 与 $ b $,用直尺和圆规作等腰三角形 $ ABC $,使底边 $ BC = a $,顶角平分线 $ AD = b $。

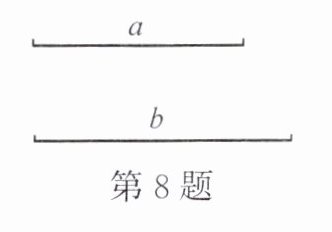
答案： 1. 作线段 $ BC = a $。
2. 分别以 $ B $、$ C $ 为圆心，大于 $ \frac{1}{2}BC $ 的长为半径画弧，两弧交于两点，过这两点作直线，交 $ BC $ 于点 $ D $（即 $ D $ 为 $ BC $ 中点，该直线为 $ BC $ 的垂直平分线）。
3. 在 $ BC $ 的垂直平分线上，以 $ D $ 为端点截取 $ DA = b $，得点 $ A $。
4. 连接 $ AB $、$ AC $，则 $ \triangle ABC $ 即为所求。