第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 写出下列命题的逆命题,并判断逆命题的真假。
(1)直角三角形的两个锐角互余。
(2)直角三角形斜边上的中线等于斜边的一半。
(1)直角三角形的两个锐角互余。
(2)直角三角形斜边上的中线等于斜边的一半。
答案:
1.
(1)两锐角互余的三角形是直角三角形,真命题
(2)一边上的中线等于这条边一半的三角形是直角三角形,真命题
(1)两锐角互余的三角形是直角三角形,真命题
(2)一边上的中线等于这条边一半的三角形是直角三角形,真命题
2. 阅读教科书中的本节内容后回答:
(1)请梳理直角三角形的判定方法。
(2)观察例2图中的$\triangle DAC与\triangle BDC$的形状,当两个等腰三角形的顶角互补时,它们的底角有什么数量关系?
(3)如图,$CD是\triangle ABC的边AB$上的中线,延长$CD至点E$,使$DE = CD$,连结$BE$,请你证明$\triangle ABC$是直角三角形。
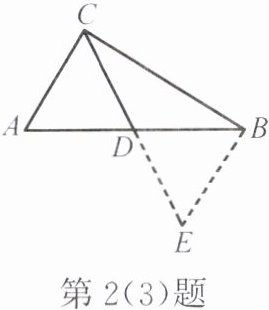
(1)请梳理直角三角形的判定方法。
(2)观察例2图中的$\triangle DAC与\triangle BDC$的形状,当两个等腰三角形的顶角互补时,它们的底角有什么数量关系?
(3)如图,$CD是\triangle ABC的边AB$上的中线,延长$CD至点E$,使$DE = CD$,连结$BE$,请你证明$\triangle ABC$是直角三角形。

答案:
2.
(1)一个直角、两锐角互余
(2)互余
(3)提示:先证△ADC≌△BDE,得AC=BE及AC//BE,再证△ABC≌△ECB
(1)一个直角、两锐角互余
(2)互余
(3)提示:先证△ADC≌△BDE,得AC=BE及AC//BE,再证△ABC≌△ECB
3. 阅读教科书中的本节内容后回答:
(1)如图,已知$D是\triangle ABC的边AB$上的一点,$\triangle ACD和\triangle BCD$都是等腰三角形,则$\triangle ABC$的形状是
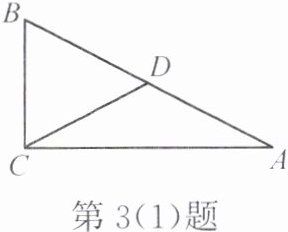
(2)在$\triangle ABC$中,若$\angle A+\angle B= \angle C$,则这个三角形是
(3)已知一个三角形的三个内角的度数之比为$1:2:3$,请判断这个三角形的形状,并说明理由。
(1)如图,已知$D是\triangle ABC的边AB$上的一点,$\triangle ACD和\triangle BCD$都是等腰三角形,则$\triangle ABC$的形状是
直角三角形
。
(2)在$\triangle ABC$中,若$\angle A+\angle B= \angle C$,则这个三角形是
直角三角形
。(3)已知一个三角形的三个内角的度数之比为$1:2:3$,请判断这个三角形的形状,并说明理由。
直角三角形,理由略
答案:
3.
(1)直角三角形
(2)直角三角形
(3)直角三角形,理由略
(1)直角三角形
(2)直角三角形
(3)直角三角形,理由略
查看更多完整答案,请扫码查看


