《2025年预学与导学八年级数学上册浙教版》

1. 张师傅做小商品生意。第一次进货时,他以每件 $a$ 元的价格购进了 20 件甲商品,以每件 $b$ 元的价格购进了 30 件乙商品($a ＞ b$)。根据市场行情,他将这两种商品都以每件 $\frac{a + b}{2}$ 元的价格出售。在这次买卖中,张师傅(A)。
A.赚钱
B.不赚不赔
C.赔钱
D.无法确定赚或赔

答案： A

2. 已知 $a$,$b$ 为有理数,给出下列结论：
①若 $a ＞ b(ab \neq 0)$,则 $\frac{1}{a} ＜ \frac{1}{b}$；
②若 $a + b = 0(b \neq 0)$,则 $\frac{a}{b} = -1$；
③若 $ab ＞ 0$,则 $|a + b| = |a| + |b|$；
④$a^2 \geq a$。
其中结论正确的是②③。

答案： ②③

3. (1) 完成下列填空：
|已知|填“＞”或“＜”

（＞）（＜）
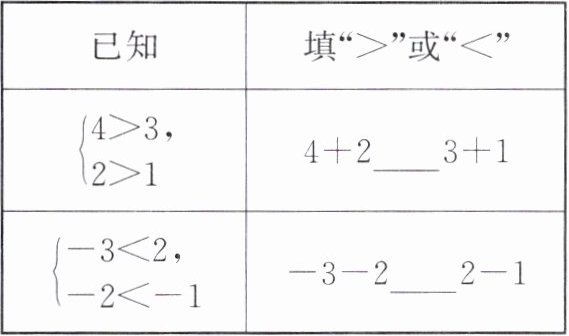
(2) 一般地,如果 $\begin{cases}a ＜ b \\ c ＜ d\end{cases} $,那么 $a + c$＜$b + d$。(填“＞”或“＜”)请你利用不等式的基本性质,说明上述不等式的正确性。
结论:a+c＜b+d。理由:因为a＜b,所以a+c＜b+c。因为c＜d,所以b+c＜b+d。所以a+c＜b+d。

答案： （1）＞ ＜ （2）＜,结论:a+c＜b+d。理由:因为a＜b,所以a+c＜b+c。因为c＜d,所以b+c＜b+d。所以a+c＜b+d。故答案为“＜”

4. (1) 如果 $x ＞ y$,请比较 $(a - 3)x$ 与 $(a - 3)y$ 的大小,并说明理由。
小贴士：注意 $a$ 可以取哪些数。

当a＞3时,(a-3)x＞(a-3)y;当a=3时,(a-3)x=(a-3)y;当a＜3时,(a-3)x＜(a-3)y
(2) 如果关于 $x$ 的不等式 $(m - 1)x ＞ m - 1$ 可化为 $x ＜ 1$,那么 $m$ 的取值范围是m＜1。

答案： （1）当a＞3时,(a-3)x＞(a-3)y;当a=3时,(a-3)x=(a-3)y;当a＜3时,(a-3)x＜(a-3)y （2）m＜1

5. 根据不等式的基本性质,我们可以得到比较两数大小的方法：
若 $a - b ＞ 0$,则 $a ＞ b$；
若 $a - b = 0$,则 $a = b$；
若 $a - b ＜ 0$,则 $a ＜ b$。
反之也成立。
这种比较大小的方法称为“求差法”。请运用这种方法尝试解决下列问题：
(1) 若 $a ＜ b$,则 $2a + 2b - 1$＞$3a + b$。
(2) 试比较 $\sqrt{3}$ 与 $2\sqrt{2} - \sqrt{3}$ 的大小。
$\sqrt{3}＞2\sqrt{2}-\sqrt{3}$
(3) 比较 $4 + 3a^2 - 2b + b^2$ 与 $3a^2 - 2b + 1$ 的大小。
因为$(4+3a²-2b+b²)-(3a²-2b+1)=b²+3＞3＞0$,所以$4+3a²-2b+b²＞3a²-2b+1$
(4) 若 $a ＞ b ＞ 0$,求证：$a^2 ＞ b^2$。
因为$a＞b＞0$,所以$a+b＞0$,$a-b＞0$,而$a²-b²=(a+b)(a-b)＞0$,所以$a²＞b²$

答案： （1）＞ （2）√3＞2√2-√3
（3）因为(4+3a²-2b+b²)-(3a²-2b+1)=b²+3＞3＞0,所以4+3a²-2b+b²＞3a²-2b+1
（4）因为a＞b＞0,所以a+b＞0,a-b＞0,而a²-b²=(a+b)(a-b)＞0,所以a²＞b²