《2025年预学与导学八年级数学上册浙教版》

1. 若关于$x的不等式组\begin{cases}x \leq 2,\\x ＜ a\end{cases} 的解是x \leq 2$,则$a$的取值范围是a＞2。

答案： a＞2

2. 若关于$x的不等式组\begin{cases}x - m ＜ 0,\\7 - 2x \leq 1\end{cases} $的整数解共有4个,则$m$的取值范围是6＜m≤7。
小贴士：可借助数轴进行分析。

答案： 6＜m≤7

3. 已知$a$,$b$为实数,则解为$-2 ＜ x ＜ 2$的不等式组是(D)。
A.$\begin{cases}ax ＞ 1,\\bx ＞ 1\end{cases} $
B.$\begin{cases}ax ＞ 1,\\bx ＜ 1\end{cases} $
C.$\begin{cases}ax ＜ 1,\\bx ＞ 1\end{cases} $
D.$\begin{cases}ax ＜ 1,\\bx ＜ 1\end{cases} $

答案： D

4. 先阅读例题,再按要求完成作业。
例题：解不等式$(3x - 2)(2x + 1) ＞ 0$。
解：由有理数的乘法法则“两数相乘,同号得正”可知
①$\begin{cases}3x - 2 ＞ 0,\\2x + 1 ＞ 0\end{cases} $或②$\begin{cases}3x - 2 ＜ 0,\\2x + 1 ＜ 0;\end{cases} $
解不等式组①,得$x ＞ \frac{2}{3}$,
解不等式组②,得$x ＜ -\frac{1}{2}$。
所以不等式$(3x - 2)(2x + 1) ＞ 0的解是x ＞ \frac{2}{3}或x ＜ -\frac{1}{2}$。
请根据上述方法,求不等式$\frac{5x + 1}{2x - 3} ＜ 0$的解集。

答案： -1/5＜x＜3/2

5. 如图所示为一个运算流程：

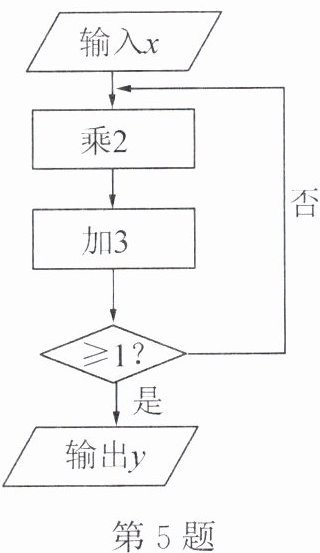
(1) 当$x = 2$时,$y = $7；当$x = -2$时,$y = $1。
(2) 若需要经过两次运算才能输出$y$,求$x$的取值范围。
$-2≤x＜-1$
(3) 若无论经过多少次运算都无法输出$y$,试探究$x$的取值范围。
$x≤-3$

答案： （1）7 1
（2）-2≤x＜-1
（3）x≤-3