《2025年预学与导学八年级数学上册浙教版》

1. 下列条件中,可以判定一个三角形为等腰三角形的是(B)。
A.三条边长分别是 $ 5 $,$ 5 $,$ 11 $
B.周长为 $ 14 $,其中两边长分别是 $ 4 $,$ 5 $
C.三条边长的比是 $ 1:1:3 $
D.周长为 $ 24 $,其中两边长分别是 $ 6 $,$ 12 $

答案： B

2. 下列说法中,正确的是(D)。
A.等腰三角形的对称轴是角平分线
B.等腰三角形的对称轴是角平分线所在的直线
C.等腰三角形的对称轴是顶角平分线
D.等腰三角形的对称轴是顶角平分线所在的直线

答案： D

3. 若等边三角形的边长为 $ a $,则它的周长为3a。等边三角形共有3条对称轴。

答案： 3a 3

4. (1) 若一个等腰三角形的底边长为 $ 6 cm $,一条腰长为 $ 8 cm $,则它的周长是22cm。
(2) 若一个等腰三角形的一边长是 $ 4 cm $,另一边长是 $ 10 cm $,则它的周长是24cm。
＜小贴士：等腰三角形的三边应满足什么条件？＞

答案：
(1)22cm　
(2)24cm　小贴士:略

5. 若实数 $ a $,$ b $ 满足 $ |a - 7| + \sqrt{b - 11} = 0 $,则以 $ a $,$ b $ 的值为两边长的等腰三角形的周长是25或29。

答案： 25或29

6. 若等腰三角形的底边长为 $ 6 $,则腰长 $ a $ 的取值范围是a＞3。

答案： a＞3

7. 已知一个等腰三角形的两边长是两个连续的偶数,周长为 $ 20 $,则该等腰三角形的腰长是6。

答案： 6

8. 用 $ 10 $ 根等长的火柴棒搭成一个等腰三角形(不允许折叠或重叠,火柴棒不能折断)。要求：至少画出一个这样的等腰三角形。

答案： 边长为2,4,4或4,3,3

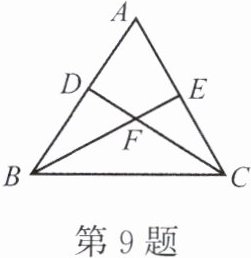
9. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,点 $ D $,$ E $ 分别在边 $ AB $,$ AC $ 上,$ AD = AE $,$ DC $ 与 $ BE $ 交于点 $ F $,则图中全等的三角形有3对。选择其中一对进行证明。

证明略

答案： 3　证明略